МЕТОДИЧЕСКАЯ РАЗРАБОТКА «Рекомендации по проведению и проверке математического диктанта»

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

«Рекомендации по проведению и проверки математического диктанта»

 Зачем нужны математические диктанты?

Математические диктанты – одна из форма контроля знаний. Но употребляются они всё же редко, так как учащимся трудно воспринимать задания на слух. Одной из важнейших задач в обучении является формирование у детей умения получать информацию на слух, запоминать на слух, обрабатывать и преобразовывать информацию. Из имеющихся в нашем распоряжении органов чувств, воспринимающих информацию, слуховой орган занимает второе место после зрительного, поэтому развивать его возможности у детей крайне важно. Использование математических диктантов помогает в решении этих задач. 
Если диктанты проводить часто , то школьники приучаются воспринимать задания на слух. А ценность такого умения очень важна в жизни . Оно приводит к умению слушать собеседника , телепередачу , слушать лекцию.

Математические диктанты проводятся со следующими целями.

Прежде всего, они помогают контролировать знания, умения и навыки учащихся. Проанализировав диктанты, учитель получает достаточно подробную информацию об уровне усвоения пройденного как отдельными учащимися, так и классом в целом. Это позволяет оперативно устранять пробелы в подготовке учащихся.

Однако ещё более важно то, что математические диктанты играют обучающую роль. Выслушав фразу диктанта, учащиеся выполняют определенную работу – записывают алгебраическое выражение выполняют указанное построение. При этом требуется не только воспроизвести заученную формулировку, а творчески подойти к заданию.

Диктанты способствуют и развитию навыков логического мышления, и выработке умения работать с чертежными инструментами. 
Известная не шаблонность постановки задачи и ограниченность времени на выполнение задания дисциплинируют учащихся, приучают к собранности, сосредоточенности, целеустремленности. 
Проведение математических диктантов способствует и повышению общей грамотности учащихся.В результате систематического использования этой формы работы резко уменьшается количество ошибок в написании математических терминов.

 Достоинства и недостатки математических диктантов .

недостатки математических диктантов .

• не по любой теме можно провести диктант,

• не все учащиеся способны хорошо воспринимать задания на слух ,

• с их помощью можно проверить, усвоили ли учащиеся обязательный минимум знаний, но нельзя организовать углубленную проверку.

Но наряду с недостатками можно отметить и достоинства:

• математические диктанты развивают умение воспринимать задания на слух, а это ведет к умению слушать лекцию и слушать вообще,

• это альтернатива устного счета, который охватывает не всех учеников,

• ответы на вопросы диктанта показывают, усвоено ли основное содержание ранее изложенного материала.

Как организовать проведение математического диктанта. 

Математические диктанты являются одной из форм письменной работы. В зависимости от текста он проводится 8-15 минут. Поэтому проводить его следует либо в начале урока,либовконце. 

Для диктантов лучше использовать листы бумаги (бланки ответов). Можно использовать при проведении диктанта два бланка ответов для того, чтобы ученик мог один бланк сдать учителю, а второй использовать для проверки правильности выполнения работы. Если есть закрытые доски, то можно, либо написать ответы заранее, либо вызвать два ученика к доске и их ответы проверить вместе с классом. Проверка сразу на уроке даёт возможность ещё раз закрепить изученный материал.

Во время проверки напротив правильного ответа ученик ставит «+», напротив ошибочного – «минус», напротив ответа с недочетом -  «плюс, минус». Можно при проверке обменяться работами с соседом по парте.

Ó÷èòåëü äîëæåí äèêòîâàòü âîïðîñû ÷åòêî, ãðîìêî, äåëàòü äîñòàòî÷íûå ïàóçû, ÷òîáû äåòè óñïåëè çàïèñàòü îòâåòû. Âîïðîñ íåîáõîäèìî ÷èòàòü ïî äâà ðàçà, êàæäûé âàðèàíò ïî î÷åðåäè. ×òîáû äåòè íå ïóòàëè âàðèàíòû, ìîæíî âûïîëíèòü àóäèîçàïèñü òåêñòà äèêòàíòà, ïåðâûé âàðèàíò – æåíñêèì ãîëîñîì, âòîðîé – ìóæñêèì. Ó÷åíèê ñêîðî âîîáùå ïåðåñòà¸ò ðåàãèðîâàòü íà “íå ñâîé” ãîëîñ: ñïîêîéíî ðàáîòàåò, ïîêà äèêòóåòñÿ çàäàíèå äðóãîãî âàðèàíòà, è íåìåäëåííî âêëþ÷àåòñÿ â ðàáîòó, êàê òîëüêî íà÷èíàåòñÿ ÷òåíèå çàäàíèÿ åãî âàðèàíòà. Èñïîëüçîâàíèå çâóêîçàïèñåé ÷ðåçâû÷àéíî äèñöèïëèíèðóåò êëàññ: ó÷åíèê ïîíèìàåò, ÷òî ìàøèíå âñ¸ ðàâíî, óñïåë ëè îí. Ïîýòîìó ñáîè ñòàíîâÿòñÿ ðåäêèìè. Åñëè íåò òàêîé âîçìîæíîñòè, ìîæíî ñäåëàòü ñëåäóþùåå: êîãäà ó÷èòåëü äèêòóåò âîïðîñû ïåðâîãî âàðèàíòà, îí ñòàíîâèòñÿ ïåðåä ó÷àùèìèñÿ, ñèäÿùèì íà ïåðâîé ïàðòå íà ïåðâîì âàðèàíòå, à êîãäà äèêòóåò âîïðîñû âòîðîãî âàðèàíòà, îí ñòàíîâèòñÿ ïåðåä ó÷àùèìèñÿ, ñèäÿùèìè íà ïåðâîé ïàðòå íà âòîðîì âàðèàíòå, èëè êîãäà ó÷èòåëü äèêòóåò âîïðîñû ïåðâîãî âàðèàíòà, îí äåðæèò â ðóêàõ ëèñò ñ öèôðîé 1, à êîãäà äèêòóåò âîïðîñû âòîðîãî âàðèàíòà, îí äåðæèò â ðóêàõ ëèñò ñ öèôðîé 2 .

Как выставлять оценки за диктанты 
Оценки за работу выставляются с учётом числа верно выполненных заданий. Целесообразно перед началом диктанта довести до сведения учащихся нормы оценок. Если в диктанте 10 заданий, оценки могут быть такими: 
Например: 

Число верных ответов	Оценка
10-9	5
8-6	4
5-3	3
менее 3	2

Учитель может – исходя из особенностей учащихся класса, может использовать свои подходы к оцениванию результатов диктанта. Иногда вопросы диктанта по значимости и содержанию можно разделить на “лёгкие” и “трудные”. В этом случае есть смысл каждый вопрос оценить в баллах (например, от 1 до 3 баллов), тогда итоговая оценка выставляется по сумме баллов. 

Если Вы в своей работе не применяете математические диктанты, значит для этого есть причины: Много времени тратится на подготовительную работу. Проведение диктанта требует от учителя весьма большого напряжения: надо читать в оптимальном темпе тексты заданий, следить за классом, реагировать на практически неизбежные сбои.

ПРИЛОЖЕНИЕ

5 класс.

Диктант по теме: «Признаки делимости на 9 и на3.»

1. Закончите предложение: «Число делится на 9 ( 3 ), если сумма цифр числа…»

2. Пользуясь признаками делимости на 3, определите, делятся ли числа 3213, 78213, 43552, 117 ( 2511, 65031, 45083 450) на 3? 

3. Пользуясь признаками делимости на 9 , определите, делятся ли числа 3213, 78213, 43552, 117( 2511, 65031, 45083 450) на 9? 

4. 4. Какие цифры можно подставить вместо звездочки в запись числа   641 * 2   , чтобы
   это число делилось на девять (три)? 

5. Какие цифры можно подставить вместо звездочки в запись числа   973 *   , чтобы это число не было кратно трем (девяти)?

6. Напишите наименьшее четырехзначное число, чтобы это число делилось на девять (три)? 

7. Напишите наибольшее трехзначное число, чтобы это число не делилось на девять (три)? 

Диктант по теме: «Процент.»

1. Закончите предложение: «Один процент – это…» (« Процентом называется…»).

2. Запишите в виде десятичной дроби 32% (25%).

3. Запишите в процентах десятичную дробь 0,25 (0,32).

4. Сколько процентов число 1 составляет от числа 5 ( 4 от 20)?

5. Как называется один процент центнера ( 0,1% от тонны)?

6. Найдите 25% от 8 км ( 40% от 15 км).

7. Найдите 15%от 25 руб. (30% от 50руб.)

8. В коробке 3 красных и 67 синих карандашей. Сколько % от всех

карандашей составляют синие (красные) карандаши?

Диктант по теме: «Прямоугольный параллелепипед.»

1. Закончите предложение: «У  прямоугольного параллелепипеда противоположные грани — …» («Куб — это прямоугольный параллелепипед, …»).

2. Сколько проволоки потребуется для изготовления каркаса куба с ребром 6см ( 8см)?

3. Сколько в прямоугольном параллелепипеде вершин (ребер)?

4. Может ли только одна грань прямоугольного параллелепипеда являться квадратом (не являться квадратом) ?

5. Сколько в прямоугольном параллелепипеде граней(вершин)?

6. Используя размеры прямоугольного параллелепипеда вычислите площадь поверхности:

а = 2 м а = 6 см

в = 5 м в = 5 см

с = 4 м с = 3 см

7. Сколько в прямоугольном параллелепипеде ребер (граней)?

6 класс.

Диктант по теме: «Основное свойство пропорций.»

1. Закончите предложение: «Равенство двух отношений называют…. («Если пропорция верна, то произведение ее крайних членов равно …»).

2. Êàê íàçûâàþòñÿ ÷èñëà õ è ó (à è â ) â ïðîïîðöèè õ:à=â:ó?

3. ×èñëî âîñåìíàäöàòü òàê îòíîñèòñÿ ê ÷åòûðåì, êàê äâàäöàòü ñåìü îòíîñèòñÿ ê øåñòè. Çàïèøèòå ïðîïîðöèè

4. Íàéòè íåèçâåñòíûé ÷ëåí ïðîïîðöèè: õ:14=36:7 (õ:12=36:18 ).

5. На участке дороги плиты длинной 6 м заменили новыми длиной 8 м. Сколько нужно новых плит для замены 240 старых?

6. Âåðíà ëè ïðîïîðöèÿ:    ( ). 

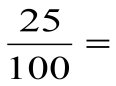
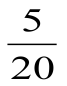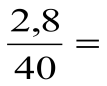
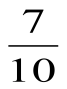7. Три ученика пропололи грядку за 4ч. За сколько часов выполнят 
работу два (четыре) ученика?

Диктант по теме: «Умножение.»

1. Óìíîæüòå 3 íà -4 (-5 íà 0).

2. Óìíîæüòå -3 íà 0 (-8 íà -3).

3. Ðåøèòå óðàâíåíèå: õ / 6 = ( -3 ), õ / ( - 4) = 8

4. Ïðîäîëæèòå ïðåäëîæåíèå: «×òîáû óìíîæèòü îòðèöàòåëüíîå ÷èñëî íà ïîëîæèòåëüíîå, íàäî…» («×òîáû ïåðåìíîæèòü äâà îòðèöàòåëüíûõ ÷èñëà, íàäî…»).

5. Âåðíî ëè âûñêàçûâàíèå (îòâåòüòå «äà» èëè «íåò»): «Ïðîèçâåäåíèå äâóõ îòðèöàòåëüíûõ ÷èñåë — ïîëîæèòåëüíîå ÷èñëî» («Ïðîèçâåäåíèå äâóõ öåëûõ ÷èñåë íå ìîæåò áûòü ìåíüøå êàæäîãî èç ìíîæèòåëåé»).

6. Ðåøèòå óðàâíåíèå: ó ( ó – 4) = 0, õ ( õ +5) = 0

7. Âû÷èñëèòå çíà÷åíèå âûðàæåíèÿ ó*(- 16) ïðè ó=3 (11õ ïðè õ= -5 )

7 класс. Геометрия.

Диктант по теме: «Вертикальные углы.»

1. Продолжите предложение: «Два угла называются вертикальными, если…»( «Если стороны одного угла являются продолжением сторон другого угла, то такие углы…» )

2. Чему равен угол, вертикальный углу в 47⁰( 123⁰ ) ?

3. У двух углов общая вершина, каждый из этих углов равен 60⁰ (40⁰). 0бязательно ли эти углы вертикальные?

4. Может ли при пересечении двух прямых образоваться четыре тупых (острых) угла?

5. Сумма двух углов, образованных при пересечении двух прямых, равна 150⁰(170⁰ ). Могут эти углы быть вертикальными?

6. Один из углов, которые получаются при пересечении двух прямых, равен 40⁰ (120⁰ ). Найдите остальные углы.

7. Один из углов, которые получаются при пересечении двух прямых в 3 раза больше другого. Найдите эти углы.

8. Один из двух углов, который получается при пересечении двух прямых, в 8 раз меньше другого. Найти эти углы.

Диктант по теме: «Прямая и отрезок.»

Первый вариант.

1. Начертите прямую и обозначьте ее буквой а.

2. Отметьте точку D, не лежащую на прямой а.

3. Отметьте точку С, лежащую на прямой а.

4. Запишите символами предложение: «Точка С лежит на прямой b, а точка D не лежит на ней».

5. Даны две прямые а и b , пересекающиеся в точке С, и точка D,

отличная от точки С и лежащая на прямой а.

а) Выполните построение и запишите условие символами.

б) Может ли точка D лежать на прямой b?

6. На прямой b возьмите точки K, L, M. Запишите все образовавшиеся отрезки.

7. На плоскости даны три точки. Сколько прямых можно провести через эти точки так, чтобы на каждой прямой лежали хотя бы две из данных точек? Рассмотрите все возможные случаи и сделайте рисунки.

Второй вариант.

1. Начертите прямую и обозначьте её буквой b.

2. Отметьте точку М ,лежащую на прямой b.

3. Отметьте точку D, не лежащую на прямой b.

4. Используя математические символы запишите предложение : «Точка М лежит на прямой b ,а точка D не лежит на ней».

5. Начертите прямые а и b, пересекающиеся в точке К. На прямой а отметьте точку С , отличную от точки К.

а) Являются ли прямые КС и а различными прямыми ?

б) Может ли прямая b проходить через точку С?

1. На прямой а возьмите точки С, D ,Е. Запишите все образовавшиеся отрезки.

7. Сколько точек пересечения могут иметь три прямые? Рассмотрите все возможные случаи и сделайте соответствующие рисунки.

7 класс. Алгебра.

Диктант по теме: «Умножение многочленов.»

1. Ïðîäîëæèòå ïðåäëîæåíèå: «×òîáû óìíîæèòü ìíîãî÷ëåí íà ìíîãî÷ëåí, íóæíî …» («Â ðåçóëüòàòå óìíîæåíèÿ ìíîãî÷ëåíà íà ìíîãî÷ëåí …»).

2. Âûïîëíèòå äåéñòâèÿ: (3n ² – 2) (1 – 4 n) =; (a – 2) (3 + a) =; (3 – 4c)(2c ² – c – 1)=;(ñ + 5) (2c – 1) =.

3. Çàìåíèòå áóêâó «Ì» ìíîãî÷ëåíîì òàê, ÷òîáû ïîëó÷åííîå ðàâåíñòâî áûëî âåðíûì: 5à + Ì = 5à + 3b – 8; ( b² – bc -  Ì = b² – bc – 7b + 5;)        

4.  Óìíîæüòå ìíîãî÷ëåí õ – ó ( à + â ) íà ìíîãî÷ëåí õ +ó ( à – â ).

5. Óìíîæüòå ìíîãî÷ëåí õ + ó ( à - â ) íà ìíîãî÷ëåí x ² – õó + ó ²  (à²+ àâ + b²

6. Ïðåäñòàâüòå â âèäå ñòàíäàðòíîãî ìíîãî÷ëåíà êâàäðàò äâó÷ëåíà õ -2ó , ( à + 5â).

8класс. Алгебра.

Диктант по теме: «Функция у = х² , ее график.»

1. Êàêàÿ èç ôóíêöèé íàçûâàåòñÿ êâàäðàòè÷íîé? Êàê íàçûâàåòñÿ ôóíêöèÿ ó = õ2? 2. Óêàæèòå íîìåð ôóíêöèè, êîòîðàÿ íå ÿâëÿåòñÿ êâàäðàòè÷íîé
1 âàðèàíò 1) ó = 5õ2 + 3õ 2) ó = 5õ + 2õ2– 2 3) ó = 4õ + 7  4) ó = –3õ2 – 4 5) ó = 5/õ2	2 âàðèàíò 1) ó = 4õ + 3õ2 2) ó = 2õ – 6õ2 3) ó = – 6õ + 10 4) ó = 4õ2 + 7  5) ó = 3õ – õ2 + 9

3. Функция задана формулой у = х² . Чему равно ее значение при х= -5 ( 6 ).

4. Принадлежит ли точка (-3, 9), [( - 4, 15)] графику функции у = х².

5. Значении функции у = х² при х = 12 ( -15 ) равно 144 ( 225 ), чему оно будет равно при х = -12 ( 15 ).

6. Аргумент равен -2. Найдите значение квадратичной функции у = х² + 3х – 5,

(у = 2х² – х + 4 ).

7. Найдите значение аргумента квадратичной функции у = х² – 9 (у = х² – х – 6),

если значение функции равно 0.