Пояснительная записка.
В 2020 -2021учебном году промежуточную аттестацию по геометрии в 8 классе рекомендуем организовать в форме устного экзамена.
Целью устного экзамена является проверка уровня предметной компетентности учащихся 8 классов по геометрии за курс 8 класса.
Основные цели изучения геометрии:
Развитие пространственных представлений, что в требованиях, предъявляемых к знаниям и умениям учащихся стандартом, формулируется как умение:
читать и делать чертежи, необходимые для решения;
выделять необходимую конфигурацию при чтении чертежа;
определять необходимость дополнительных построений при решении задач и выполнять их;
различать взаимное расположение геометрических фигур.
Формирование и развитие логического мышления, что в требованиях, предъявляемых к знаниям и умениям учащихся стандартом, формулируется как владение методами доказательств, применяемыми при обосновании геометрических утверждений (теорем, лемм, следствий и т.д.), а также при проведении аргументации и доказательных рассуждений в ходе решения задач.
Структура экзаменационного билета.
Билеты содержат три вопроса по различным темам курса геометрии за 8 класс (два теоретических вопроса и одна задача).
Первый вопрос. Базовый уровень.
В первом вопросе от учащихся требуется выполнить одно из трех возможных заданий: первое – дать определение фигуры; второе – воспроизвести одну из формул для вычисления длин отрезков, градусных мер углов, площадей; третье – воспроизвести формулировку одной из теорем о свойствах или признаках фигур, их элементов, отношениях фигур.
При ответе на первый вопрос учащиеся должны:
- дать четкое определение фигуры, включающее в себя как вербальное определение, так и графическое – чертеж, а также привести пример применения этого определения, верно иллюстрирующий его смысл.
-правильно воспроизвести одну из формул для вычисления значений геометрических величин (площадей), при этом, кроме записи формулы, необходимо выполнить чертеж и объяснить смысл формулы. Привести пример применения этой формулы, позволяющий сделать вывод об уровне сформированности умения применять эту формулу.
- воспроизвести формулировку теоремы, проиллюстрировав содержание теоремы выполнением чертежа; привести пример применения этой теоремы, верно отражающий ее содержание и смысл.
Второй вопрос. Продвинутый уровень.
Во втором вопросе учащиеся должны, как правило, дать определение фигуры, сформулировать ее свойство или признак, указанный в теореме, и доказать эту теорему.
При ответе на второй вопрос учащиеся должны:
дать определение фигуры, включающее в себя как вербальное определение, так и графическое – чертеж;
правильно воспроизвести формулировку теоремы, проиллюстрировав ее выполнением чертежа по условию теоремы;
привести доказательство теоремы, при этом доказательство считается выполненным верно, если учащийся правильно привел схему доказательства, обосновал все логические шаги, выполнил чертежи, которые правильно отражают, кроме условия, еще и ход доказательства.
Практическая часть. Третий вопрос билета – задача. Цель включения этих заданий – проверка овладения учащимися основными практическими умениями, полученными в ходе изучения курса, эти задачи соответствуют уровню базовой подготовки.
С помощью заданий третьих вопросов проверяются знание и понимание важных элементов содержания (геометрических понятий, свойств основных фигур, отношений между фигурами, методов доказательств и пр.), владение основными формулами, умение применять полученные знания к решению геометрических задач. При выполнении этих заданий учащиеся также должны продемонстрировать определенную системность знаний и широту представлений, узнавать стандартные задачи в разнообразных формулировках.
Время подготовки выпускника. Система оценивания ответа.
Примерное время, отводимое на подготовку выпускника к ответу, – 20–30 минут.
Оценивание ответа осуществляется по традиционной пятибалльной шкале. Ученик у доски отвечает на теоритические вопросы, дополняя свой ответ необходимыми чертежами и записями. Далее на доске рассматривается подробное решение задач, с ссылками на все используемые факты.
Критерии оценивания:
Отметка 5 (отлично) – ставится за полный, логически обоснованный ответ на все три вопроса билета.
Отметка 4 (хорошо) – выставляется за обоснованный полный ответ, но с допущением 1-2 негрубых недочетов на 1-2 вопросы с доказательством и решение задачи;
Отметка 3 (удовлетворительно) – ставится за решение задачи и правильно сформулированные теоремы, свойства, определения первого и второго вопросов (без доказательства).
Отметка 2 (неудовлетворительно) – выставляется во всех остальных случаях.
Вопросы без доказательства:
Сформулируйте определение многоугольника. Элементы многоугольника. Виды многоугольников. Сформулировать теорему о сумме углов выпуклого многоугольника.
Сформулируйте определение трапеции. Виды трапеции.Сформулируйте свойства равнобедренной трапеции.
Сформулировать определение квадрата и перечислить все его свойства.
Приведите формулы площадей ромба, квадрата, параллелограмма, трапеции. Для ромба приведите несколько формул.
Сформулируйте определение подобных треугольников. Сформулируйте признаки подобия треугольников.
Сформулируйте теорему Фалеса. Начертите чертеж.
Сформулируйте утверждения о пропорциональных отрезках в прямоугольном треугольнике.
Сформулируйте определение синуса, косинуса и тангенса острого угла прямоугольного треугольника. Запишите основное тригонометрическое тождество.
Сформулируйте определение окружности. Взаимное расположение прямой и окружности. Сформулируйте определение касательная к окружности и свойство касательной.
Сформулируйте свойство отрезков касательных, проведенных из одной точки.
С![]() формулируйте формулу нахождения величины угла между пересекающимися хордами через дуги окружности.
формулируйте формулу нахождения величины угла между пересекающимися хордами через дуги окружности.
С![]() формулируйте формулу нахождения величины угла между секущими, пересекающимися вне окружности
формулируйте формулу нахождения величины угла между секущими, пересекающимися вне окружности
Назовите формулу Герона. В каких случаях данную формулу применяют?
Назовите значение синуса, косинуса и тангенса для углов 30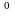 , 45
, 45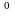 , 60
, 60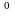 .
.
Сформулируйте определения центрального угла окружности и угла, вписанного в окружность. Сформулируйте теорему об измерении вписанного угла и следствия из нее.
Сформулируйте условия, когда в четырехугольник можно вписать окружность и условие, когда около четырехугольника можно описать окружность.
Вопросы с доказательством
Сформулируйте определение параллелограмма. Сформулируйте признаки параллелограмма и докажите один признак по выбору.
Сформулируйте определение параллелограмма. Сформулируйте и докажите свойства углов и сторон параллелограмма.
Сформулируйте определение параллелограмма. Сформулируйте и докажите свойство диагоналей параллелограмма.
Сформулируйте определение ромба. Сформулируйте и докажите свойство диагоналей ромба.
Сформулируйте определение прямоугольника. Сформулируйте и докажите свойство диагоналей прямоугольника.
Приведите формулы площади прямоугольника и площади параллелограмма. Выведите одну из формул по выбору.
Запишите формулу площади треугольника и докажите теорему площади треугольника. Сформулируйте теорему об отношении площадей двух треугольников, имеющих по равному углу.
Выведите формулу площади трапеции.
Сформулируйте определение прямоугольного треугольника. Сформулируйте и докажите теорему Пифагора.
Сформулируйте определение подобных треугольников. Докажите теорему об отношении площадей подобных треугольников.
Сформулируйте определение средней линии треугольника. Сформулируйте и докажите теорему о средней линии треугольника.
Сформулируйте определение касательной к окружности. Сформулируйте и докажите свойство касательной к окружности.
Сформулируйте и докажите теорему об отрезках пересекающихся хорд.
Сформулируйте определение окружности, вписанной в многоугольник. Сформулируйте и докажите теорему об окружности, вписанной треугольник. Каким свойством обладают стороны четырехугольника, описанного около окружности?
Сформулируйте определение окружности, описанной около многоугольника. Сформулируйте и докажите теорему об окружности, описанной около треугольника. Каким свойством обладают углы четырехугольника, вписанного в окружность?
Задача.
Задачи из образовательного портала по подготовке к экзаменам «РЕШУ ОГЭ»:
16.Треугольники, четырехугольники, многоугольники и их элементы
Многоугольники
Параллелограмм
Ромб
Трапеция
17.Окружность, круг и их элементы
Касательная, хорда, секущая, радиус
Окружность, описанная вокруг многоугольника
Центральные и вписанные углы
18.Площади фигур
Квадрат
Прямоугольник
Трапеция
Параллелограмм
19.Фигуры на квадратной решётке
Многоугольники
Параллелограмм
Ромб
Трапеция
5







