Итоговое повторение курса алгебры 7-9-х классов – 21 час
Пояснительная записка
Цели:
подготовить учащихся к сдаче ГИА в соответствии с требованиями, предъявляемыми новыми образовательными стандартами.
Структура курса.
Курс рассчитан на 21 занятие. Включенный в программу материал предполагает повторение и углубление следующих разделов алгебры:
Числа и вычисления.
Алгебраические выражения.
Уравнения и системы уравнений.
Неравенства и системы неравенств.
Последовательности и прогрессии.
Функции.
Реальная математика. Теория вероятностей.
Примерное планирование итогового повторения курса алгебры 7–9-х классов.
| № | Тема | Количество часов | Форма контроля |
| 1 | Числа и вычисления. | 3 | тест |
| 2 | Алгебраические выражения. | 3 | тест |
| 3 | Уравнения, системы уравнений. | 3 | тест |
| 4 | Неравенства, системы неравенств. | 3 | тест |
| 5 | Последовательности и прогрессии. | 3 | тест |
| 6 | Функции. | 3 | тест |
| 7 | Реальная математика. Теория вероятностей. | 3 | тест |
|
| Итого: | 21 |
|
Тест «Числа и вычисления»
Расположите в порядке возрастания числа:
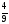 ;
; 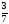 ; 0,7; 0,3
; 0,7; 0,3
1)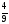 ;
; 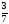 ; 0,3; 0,7 2) 0,3;
; 0,3; 0,7 2) 0,3; 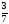 ;
;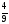 ; 0,7 3) 0,3;
; 0,7 3) 0,3;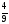 ;
; 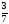 ; 0,7 4)
; 0,7 4) 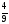 ;
; 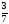 ; 0,7; 0,3.
; 0,7; 0,3.
Какому из данных промежутков принадлежит число
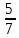 ?
?
1) [0,4; 0,5] 2) [0,5; 0,6] 3) [0,6; 0,7] 4) [0,7; 0,8]
3. Какое из чисел  ,
,  ,
,  является иррациональным?
является иррациональным?
1)  2)
2)  3)
3)  4) все эти числа
4) все эти числа
4. На координатной прямой отмечены числа а и b. Какое из следующих утверждений является верным?
![]()
ab › 0; 2) a + b ‹ 0; 3) b(a + b) ‹ 0; 4) a(a + b) ‹ 0
5. Известно, что х и у – нечётные числа. Какое из следующих чисел также является нечётным?
1) х + у; 2) 4х + у; 3) 4(х + у +1); 4) (х + 2)(у + 1)
6. На коробке с тортом имеется надпись, гарантирующая, что масса торта равна 500 ± 15 г. Какую массу при этом условии не может иметь торт?
1) 505г 2) 483г 3) 515г 4) 495г
7. Найдите десятичную дробь, равную 56,48 * 10-6.
0,05648 2) 0,005648 3) 0,00005648 4) 0,0000005648
8. Две трубы наполняют бассейн за 5,3 часа. За какое время наполнят бассейн 5 таких труб (в ч)?
1)  ; 2) 13,25; 3) 2,12 4) 0,53
; 2) 13,25; 3) 2,12 4) 0,53
9. Вычислите 
1) 120; 2)30; 3)20; 4)60.
10. Вычислить ( 5,5 - 2 ) : 4 -1.
) : 4 -1.
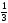 2) -
2) - 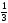 3)
3) 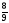 4) 9
4) 9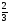 .
.
Тест «Алгебраические выражения»
Найти значение выражения
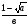 при а = 0,64; в = 0,08.
при а = 0,64; в = 0,08.
Ответ: _____________________________
При каком значении переменной x выражение
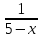 не имеет смысла?
не имеет смысла?
1)1; 2)-3; 3)5; 4)0.
Соотнесите каждое выражение с его областью определения.
А)  Б)
Б)  В)
В)  Г)
Г) 
с ≠ -3 2) с ≠ -1 3) с ≠ -3 и с ≠ -1 4) с – любое число
При каком из указанных значений х выражение
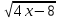 имеет смысл?
имеет смысл?
1) х = -2 2) х = -5 3) х = 5 4) х = 1
За 45 минут человек прошел 4 км. Какое расстояние он пройдет за t минут, если будет идти с той же скоростью?
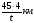 2)
2) 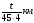 3)
3) 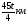 4)
4) 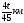
6. Из формулы s = s0 + vt выразите переменную v.
1) v =  ; 2) v =
; 2) v = 
Ответ: _____________________________
7. Представьте выражение  в виде степени.
в виде степени.
a2 2) a-4 3) a8 4) a-2
8. Найдите значение выражения (3,4 • 10-3)*(2•10-2).
6800000 2) 0,00068 3) 0,000068 4) 0,0000068
9. Упростите выражение (а + 2)2 – (4 – а2).
0 2) 2а2 3) 4а 4) 2а2 + 4а
10. Сократите дробь  .
.
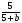 2)
2) 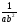 3)
3) 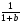 4)
4) 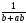
11. Упростите выражение  :
:  .
.
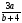 2) -
2) -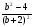 3) -
3) - 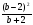 4)
4) 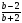
Тест «Уравнения, системы уравнений»
Решите уравнение 4х2 – 13х – 12 =0.
1)0,75; 4 2) -0,75; 4 3) 0,75; -4 4) -0,75; - 4
Найдите корни уравнения (2х – 5)(х + 3) = 0
1) 3;2,5 2) -3;2,5 3) 3; -2,5 4) -3;-2,5
Найдите сумму корней уравнения 4х2 – 12х + 5 = 0.
12 2) – 3 3) 3 4) 1,25
Соотнесите каждое квадратное уравнение и его корни:
А) х2 – 9 = 0 Б) х2 + 2х = 0 В) х2 + 4 = 0
0; -2 2) -2; 2 3) -3; 3 4) нет корней
5. Решите уравнение .
Ответ: ___________________________
6. Найдите решение системы уравнений
(-2; 1) 2) нет решений 3) (-2; -1) 4) (1; -2)
7. Найдите координаты точки пересечения параболы у = х2 -5х и прямой у = 16 + х.
Ответ: _____________________________
8. Расстояние между пристанями на реке 12 км. Катер проплыл от одной пристани до другой и вернулся обратно, затратив на весь путь 2 ч 30 мин. Какова скорость течения реки (в км/ч ), если собственная скорость катера равна 10 км/ч?
Выберите уравнение, соответствующее условию задачи, если буквой х обозначена скорость течения реки (в км/ч).
2) х =
3) 4)
9. Решите уравнение х4 – 3х3 + 4х2 – 12х = 0 Ответ: ____________
Тест «Неравенства и системы неравенств»
1. Одна из точек, отмеченных на координатной прямой, соответствует числу. Какая это точка?
1) М 2)Р 3) N 4)Q
2. О числах a и b известно, что ab. Среди приведенных ниже неравенств выберите верные:
1) a – b - 17 2) b – a 2 3) b – a a – b 17
3. Решите неравенство 6 – х 2х .
1) (-∞; -0,5] 2) [-0,5; +∞) 3) (-∞; 2] 4) [-2; +∞)
4. Решите неравенство 8х + 12 4 – 3(4 – х).
1) х -4 2) х х -5,6 4) х
5. Для каждой системы неравенств укажите номер рисунка, на котором изображено множество её решений.
А)
1)
2)
Б)
3)
В) 4)
6. Решите неравенство х2 - 9 0
1) решений нет 2) (-∞;-3) U (3; +∞) 3) (-3; 3) 4) (-∞; 3)
7. Решите неравенство х2 -2 х +1 0
Ответ: ______________________________
8. Укажите неравенство, которое не имеет решений.
1) + 5 ≥ 0 2)
+ 5 ≤ 0
3) – 5 ≤ 0 4)
- 5 ≥ 0
Тест «Последовательности и прогрессии»
Последовательность чисел
задана равенствами
и
при всех
n ≥ 2. Какое из указанных ниже чисел является членом этой последовательности?
1) 152 2) 55 3) 35 4) 25
2. Числовая последовательность задана следующими условиями:
а1 = 2; аn+1 = 3аn – 2. Найдите пятый член этой последовательности.
1) 64 2) 71 3) 81 4) 82
3. Укажите какая из нижеперечисленных последовательностей является арифметической прогрессией.
1) 2; 7; 11; 16;… 2) 5; 8; 11; 13;… 3) 7; 9; 10; 12;… 4) 10; 20; 30; 40;….
4. Каждой последовательности поставьте в соответствие формулу n-го члена.
А) 6; 12; 24… Б) 8; 6; 4… В) 2; 8; 18…
1) 10 – 2n 2) аn = 2n2 3) аn = 2n + 6 4) аn =
5. Найдите неизвестный член геометрической прогрессии
…; ; х;
; …, если
; х;
- последовательные члены и х 0.
1) 1 2) 3)
4) другой ответ
6. В первом ряду стоят 23 спортсмена, а в каждом последующем на два спортсмена больше. Сколько спортсменов в ряду с номером n?
1) 23 + 2n 2) 2n 3) 21 + 2n 4) 25 + n
7. Геометрическая прогрессия (bn) задана условиями: b1, и bn+1 = bn· . Определите формулу n-го члена этой прогрессии.
1) bn = 2) bn =
3) bn =
4) bn =
8. В геометрической прогрессии b1 = -81 , q = . В каком случае при сравнении членов этой прогрессии знак неравенства поставлен неверно?
1) b1b2 2) b1 b3 3) b2 b4 4) b3 b5
9. Найдите сумму первых шести членов арифметической прогрессии, если а1 = 12, d =3.
1) 117 2) 81 3) 78 4) 39
10. Сколько положительных членов в последовательности (сn), заданной формулой
Сn = 34 – 4n?
1) 4 2) 8 3) 9 4) 17
Тест « Функции»
1. На рисунке изображён график функции y = f(x), областью определения, которой является промежуток [-4;4]. Используя рисунок, выясните, какое из утверждений неверно.
Если x = -2, то f(x) = 3
F (-3)
f(3)
Наибольшее значение функции равно 4;
функция возрастает на промежутке [-4; -1]
2. Какая из функций является возрастающей?
у = 6х – 8 2) у = -2х + 5 3) у = 7х2 4) у = -5х2
3. Функция задана формулой y = – 5 – 8
Найдите значение функции при x = –1.
Ответ: _____.
4. Найдите координаты точки пересечения графиков функций у = (х – 3)2 + 1 и у = х2 + 4.
(2; 8) 2) (-2; 8) 3) (1; 5) 4) (3;1)
5. Каждый график соотнесите с соответствующей формулой.
А) y=; Б) y=2-x2; В) y=2x; Г) y=2x+2.
1) 2)
3)
4)
6. Найдите область определения функции у = .
1) х ≠ 1 2) х ≠ -1 3) х ≠ 1 4) х – любое число
7. Найдите координаты точек пересечения параболы y = x2 – 3x+ 2 с осями координат.
Ответ:_________________
8. График какой из функций изображен на рисунке ?
у
9. На тренировке в 50-метровом бассейне пловец проплыл 200-метровую дистанцию. На рисунке изображен график зависимости расстояния s (в метрах) между пловцом и точкой старта от времени движения t (в секундах) пловца.
Определите по графику, за какое время пловец
преодолел 130 метров.
Ответ: _______________________________________
10. Балкон имеет форму прямоугольника. С двух меньших сторон он утеплён одним слоем утеплителя, а с третьей стороны – двумя слоями. Площадь всего балкона у м2 является функцией толщины слоя утеплителя х м. После утепления балкон имеет размеры
3,6 м х 1,8 м. Задайте эту функцию формулой и выберите её из предложенных формул.
у = (2х + 3,6)(1,8 + х)
у = (х + 3,6)(х + 1,8)
у = 3,6х + 1,8х
у = (2х + 3,6)(2х + 1,8).
Тест «Реальная математика. Теория вероятностей»
1. Стоимость проезда в пригородном электропоезде составляет 198 рублей.
Школьникам предоставляется скидка 50%. Сколько рублей стоит проезд
группы из 4 взрослых и 12 школьников?
Ответ: ___________________________.
2. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с
яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того,
что пирожок окажется с яблоками.
Ответ: ___________________________.
3. Зная длину своего шага, человек может приближенно подсчитать пройденное им расстояние s по формуле s = nl, где n – число шагов, l – длина шага. Какое расстояние прошел человек, если l =60см,
n = 1200? Ответ выразите в километрах.
Ответ: ___________________________.
4. Телевизор у Маши сломался и показывает только один случайный канал. Маша включает телевизор.
В это время по 10 каналам из сорока пяти показывают новости. Найдите вероятность того, что Маша попадет на канал, где новости не идут.
1) 2)
3)
4)
.
5. На тарелке 12 пирожков: 5 с мясом, 4 с капустой и 3 с вишней. Наташа наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
1) 0,25 2) 3)
4) 3.
6. В таблице приведены средние баллы, полученные учащимися девятых классов одной из школ Санкт-Петербурга за контрольную работу по теме «Статистика».
| Класс | 9а | 9б | 9в | 9г | 9д |
| Средний балл по классу | 4,3 | 4,6 | 4,8 | 4,4 | 3,9 |
По данным таблицы определите количество классов, в которых средний балл по классу превышает средний балл всех девятиклассников школы.
1) 1 2) 2 3) 3 4) 4
| 7. На диаграмме показано содержание питательных веществ в молочном шоколаде. Определите по диаграмме, содержание каких веществ преобладает. |
| 1) белки 2) жиры 3) углеводы 4) прочее 8. Когда самолет находится в горизонтальном полете, подъемная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолета. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат – сила (в тоннах силы). Определите по рисунку, чему равна подъемная сила (в тоннах силы) при скорости 200 км/ч?
1) 1 2)100 3)200 4) 2. 9. В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Варя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Варя не найдет приз в своей банке? 1) 0,1 2) 0,5 3) 0,9 4)0,2 |
Итоговый тест
1. Средний радиус Земли приблизительно равен 6 млн. 371 тыс метров. Запишите эту величину в стандартном виде.
1) 6,371∙106 км 2) 6,371∙107 км 3) 6,371∙108 км 4) 6,371∙109 км
2. Сберегательный банк начисляет на срочный вклад 20% годовых. Вкладчик положил на счет 800 р. Какая сумма будет на этом счете через год, если никаких операций со счетом проводиться не будет?
1) 960 р. 2) 820 р. 3) 160 р. 4) 1600 р.
3. Какое из чисел является рациональным?
1) 2)
3)
4) ни одно из этих чисел
4. Найдите значение выражения 5ху + х + у - 2ху – 3ху при х = 2, у = - 3.
1) 1 2) – 1 3) 0 4) - 2
5. Укажите наибольшее из чисел:
1) 6 2) 3) 4
4) 10
6. Какое из следующих выражений равно 4 b -2?
1) 2)
3)4b- 42 4) (4b)-2.
7. Сократите дробь:
Ответ:________________
8. Решите неравенство 2х – 1 ≤ 3х + 2.
Ответ: _______________________
9. В каком случае преобразование выполнено неверно?
1) a – b +c = a – (b – c)
2) (- a)(-b)(-c)=abc
3)(a-b)(b-c) = -(a – b)c – b
4) (a - b)² = (b – a)²
10. Найдите сумму корней уравнения: .
Ответ: _______________
11. На рисунке изображены графики функций и
. Вычислите координаты точки
12. Прочитайте задачу: «От турбазы до станции турист может дойти пешком за 5 часов. На велосипеде он смог бы проехать это расстояние за 2 часа. Известно, что на велосипеде он едет со скоростью на 6 км/ч большей, чем идет пешком. Какое расстояние (в км) от турбазы до станции?»
Выберите уравнение, соответствующее условию задачи, если буквой х обозначено расстояние (в км) от турбазы до станции.
1) 2)
3)
4)
13. Последовательности заданы несколькими первыми членами. Одна из
них – арифметическая прогрессия. Укажите ее.
1) 6;7;9;12;… 2) 2;4;6;8;… 3) 2;4;8;16;… 4) 3; 1;;
| 14. На диаграмме показано содержание питательных веществ в творожных сырках. Определите по диаграмме, содержание каких веществ преобладает. |
| 1) жиры 2) белки 3) углеводы 4) прочее 15. На координатной прямой изображены числа а и с. Какое из следующих неравенств неверно?
1) |
16. Какие из следующих утверждений верны?
1) Если угол равен 750, то смежный с ним угол равен 750.
2) Через любые две точки проходит одна прямая.
3) Сумма соответственных углов 1800.
4) Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.
17. У бабушки 20 чашек: 5 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
Ответ: _____________________
18. Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии (в метрах) от дома оказался мальчик?
1) 100 2)1000 3) 1400 4) 200
Часть 2
19. Сократите дробь .
20. Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отплыл, если скорость течения реки равна 2 км/ч, а собственная
скорость лодки 6 км/ч?
21. Постройте график функции : у =



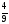 ;
; 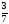 ; 0,7; 0,3
; 0,7; 0,3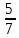 ?
? 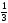 2) -
2) - 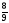 4) 9
4) 9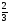 .
.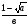 при а = 0,64; в = 0,08.
при а = 0,64; в = 0,08.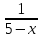 не имеет смысла?
не имеет смысла?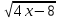 имеет смысл?
имеет смысл?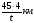 2)
2) 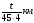 3)
3) 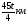 4)
4) 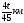
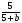 2)
2) 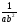 3)
3) 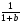 4)
4) 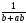
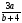 2) -
2) -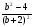 3) -
3) - 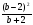 4)
4)