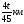Системы итогового повторения курса алгебры 7-9-х классов.
Содержание:
I. Примерное планирование учебного времени для повторения курса алгебры 7-9-х классов.
II. Тематические тестовые работы (в одном варианте).
III. Обобщающая тестовая работа (в одном варианте).
I.Примерное планирование учебного времени для повторения курса алгебры 7-9-х классов
Количество часов – 25
| № урока | Тематическое содержание | Количество часов | Вид контроля |
| 1-2 | Числа и вычисления | 2 | тест №1 |
| 3-5 | Алгебраические выражения | 3 | тест №2 |
| 6-8 | Уравнения, системы уравнений | 3 | тест№3 |
| 9-11 | Неравенства, системы неравенств | 3 | тест№4 |
| 12-14 | Последовательности и прогрессии | 3 | тест№5 |
| 15-17 | Функции и графики | 3 | тест№6 |
| 18 - 20 | Практико – ориентированные задачи | 3 | тест№7 |
| 21 – 22 | Решение упражнений по всему курсу алгебры 7-9-х классов
| 2 |
|
| 23-24 | Обобщающая тестовая работа | 2 | тест№8 |
| 25 | Анализ обобщающей тестовой работы | 1 |
|
II. Тематические тестовые работы (в одном варианте)
Тест №1 по теме «Числа и вычисления»
1. Укажите наибольшее из чисел 0,415; 0,5; 
1) 0,415; 2) 0,5; 3)  4)
4) 
2. Одна из точек, отмеченных на координатной прямой, соответствует числу  . Какая это точка?
. Какая это точка?
 8 М N 9 P Q 10
8 М N 9 P Q 10
1) точка М; 2) точка P; 3) точка Q; 4) точка N
3. Значение какой суммы меньше 2?
1) 1,602 + 0,43; 2) 0,512 + 1,501; 3) 1,305 + 0,692; 4) 0,503 + 1,497.
4. Соотнесите дроби, которые выражают доли некоторой величины, и соответствующие им проценты.
А) 0,008 Б)  В)
В)  Г) 0,08
Г) 0,08
1) 8% 2) 28% 3) 80% 4) 0,8%
Ответ
| А | Б | В | Г |
|
|
|
|
|
5.После подорожания на 25 % 1 кг черешни стал стоить 120 рублей. Сколько стоил 1 кг черешни до подорожания? Ответ: ---------------------------------------
 6. Числа b и c отмечены точками на координатной прямой. Значение какого из выражений является отрицательным? b 0 1 c
6. Числа b и c отмечены точками на координатной прямой. Значение какого из выражений является отрицательным? b 0 1 c
1) b(b – c) 2) c(c – b) 3) bc(c – b) 4) bc(b – c)
7. Вычислите  Ответ____________
Ответ____________
8. Какое из чисел  ,
,  ,
,  является иррациональным?
является иррациональным?
1) 2)
2)  3)
3)  4)Все эти числа.
4)Все эти числа.
9. Масса Луны равна 7,35 ∙ 1022 кг. Выразите массу Луны в миллионах тонн.
1) 7,35 2)7,35
2)7,35 3) 7,35
3) 7,35
10. Укажите число, равное числу 0,00038
1) 3,8∙103; 2) 3,8∙10-4; 3) 3,8∙10-5; 4) 3,8∙10-6.
Тест №2 по теме «Алгебраические выражения»
1. Найти значение выражения  при а = 0,25; в = 0,05.
при а = 0,25; в = 0,05.
Ответ: _____________________________
2. . Упростите выражение  и найдите его значение при с = -
и найдите его значение при с = - 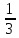 .
.
1) -3; 2) 3; 3) 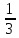 ; 4) -
; 4) - 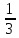 .
.
3. Соотнести каждое выражение:
А)  Б)
Б)  В)
В) 
с тождественно равным ему выражением:
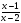 2)
2) 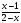 3)
3) 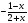 4)
4) 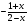
| А | Б | В |
|
|
|
|
4. Найдите второй множитель в разложении на множители квадратного трехчлена:
4х2 + 5х – 1 = (х + 1)(…)
Ответ: ____________________________
5. Какое из данных равенств является тождеством?
1) (7а – в)2 = 49а2 – в2; 2) (7а – в)2 = 49а2 – 7ав – в2; 3) (7а – в)2 = в2 – 14ав + 49а2;
4) (7а – в)2 = 49а2 + 14ав + в2.
6. Упростите выражение Ответ: ---------------------------------
Ответ: ---------------------------------
7. Из формулы s = s0 + v t выразите переменную v.
1) v =  ; 2) v =
; 2) v = 
8. За 45 минут человек прошел 4 км. Какое расстояние он пройдет за t минут, если будет идти с той же скоростью?
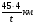 ; 2)
; 2) 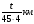 ; 3)
; 3) 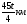 ; 4)
; 4) 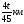
9. Найдите значение выражения (x – 8)(x – 7)(x -3)(x – 2) при x =5 - .
.
Ответ____________
Тестовая работа №3 по теме «Уравнения, системы уравнений»
1.Какое из чисел является корнем уравнения x 3 – 2x2 – 11x – 20 = 0?
1) 0; 2) 1; 3) – 1; 4) 5.
2.Решите уравнение:  = -5 Ответ: _____________________
= -5 Ответ: _____________________
3. Какое из следующих уравнений не имеет корней ?
1) х2 + 2х + 1 = 0; 2) х2 +3х + 1 = 0; 3) х2 +2х – 3 = 0 ; 4) х2 + х + 3 = 0.
4. Решите систему уравнений  Ответ: --------------------------------------
Ответ: --------------------------------------
5. Решите уравнение 3х2 + 14х – 5 = 0.
6. Прочитайте задачу: «Велосипедист от озера до деревни ехал со скоростью 15 км/ч , а обратно - со скоростью 10 км/ч. Сколько времени ушло на дорогу от озера до деревни, если на весь путь туда и обратно велосипедист затратил 1 ч?».
Пусть х ч – время на дорогу от озера до деревни. Какое уравнение соответствует условию задачи?
1)15х = 10(1 – х); 2) +
+  =1; 3) 15х + 10(1 – х) = 1; 4) 15(1 – х) = 10х.
=1; 3) 15х + 10(1 – х) = 1; 4) 15(1 – х) = 10х.
7. Прочитайте задачу: «В 5 маленьких и 7 больших коробок разложили 90 карандашей, заполнив каждую целиком. В большую коробку помещается на 6 карандашей больше, чем в маленькую. Сколько карандашей в большой коробке и сколько в маленькой?»
Пусть х – число карандашей в большой коробке, у – в маленькой коробке. Выберите систему уравнений, соответствующую условию задачи.
1)  2)
2)  3)
3)  4)
4) 
8. Решите уравнение x3 – 3x2 – x + 3 = 0. Ответ____________
9. Черешня дороже яблок на 25%. На сколько процентов яблоки дешевле черешни?
Ответ: ------------------------------------------------------------------
Тест № 4 по теме «Неравенства, системы неравенств»
1 . Известно, что а
1) в - а 1.
2. О числах  что
что  Сравните числа с и d.
Сравните числа с и d.
1) c = d 2) c d 3) c d 4) сравнить невозможно
3. Решите неравенство 3х – 4(2х – 8)
1)  ; 2) ( - 5,8; +
; 2) ( - 5,8; + 3) ( 7;
3) ( 7; ; 4) (-
.
4. Для каждой системы неравенств укажите множество её решений.
| А | В | С |
|
|
|
|
1) 2)
3)
4)
Ответ:
5. На рисунке изображен график функции у = х2 +2х. Используя график, решите неравенство х2 - 2х
1) (- 2; 0) 2) (- ∞; - 2) (0; + ∞)
3) (- ∞; - 2) 4) (0; + ∞).
6. Сколько решений системы неравенств содержится среди чисел
-5; -1; 0; 1? 1) 1 2) 2 3) 3 4) 4
7. Решить неравенство
Ответ: ---------------------------
8. Какое из чисел больше или
7 ?
9. Найдите область определения выражения .
Ответ: ---------------------------
Тест №5 по теме «Последовательности и прогрессии».
1.Последовательность задана формулой b n = n2 – 1. Какое из указанных ниже чисел является членом этой последовательности?
1) 1; 2) 2; 3) 3; 4) 4.
2. Последовательность задана формулой bn = . Сколько членов этой последовательности больше 1?
Ответ: -------------------------------
3. Каждой последовательности, заданной формулой n-го члена, поставьте в соответствие верное утверждение.
Последовательность
А. xn = n2 В. yn = 2n C. zn = 2n
Утверждение:
1) последовательность – геометрическая прогрессия
2) последовательность – арифметическая прогрессия
3) последовательность не является ни арифметической, ни геометрической прогрессией
| А | В | С |
|
|
|
|
4. Одна из данных последовательностей является арифметической прогрессией.
Укажите её.
1) 1; 2; 3; 5;… 2) 1; 2;4; 8; … 3) 1; 3; 5; 7; … 4) 1; ;
;
;…
5. Чему может быть равен знаменатель геометрической прогрессии (bn), если b5 = 6,
b8 = 48?
1) 2) 8 3) 2 4) 4
6. Подготовку к экзамену начинают с 15 мин. В каждый следующий день её время увеличивают на 10 мин. Сколько дней следует готовиться к экзамену в указанном режиме, чтобы достичь максимальной продолжительности подготовки, не влияющей на здоровье подростка, 1час 45минут?
1) 9 2) 10 4) 11 5) 12
7. В геометрической прогрессии b1 = , q = - 2. В каком случае при сравнении членов этой прогрессии знак неравенства поставлен неверно?
1) b2b3 2) b4 b3 3) b6 b4 4) b7 b5.
8. Между числами 3 и 12 вставьте три числа так, чтобы получилась геометрическая прогрессия.
9. Найдите сумму всех положительных членов арифметической прогрессии: 12,8; 12,5; …
Тест № 6 по теме «Функции и графики»
1. Функция задана формулой f(x)= -x2 + 4x -3. Найдите f(1).
4 2) 0 3) 1 4) 3.
2. Найдите область определения функции y =:
1) x ≠3; 2) x ≠ - 3; 3) x ≠0; 4) x – любое число.
3. Графики функций - 3х +2у = - 1 и 4х + 3 у =7.
1) Пересекаются в I четверти. 2) Пересекаются во II четверти;
3) Пересекаются в III четверти. 4) Пересекаются в IV четверти .
4. Вычислить координаты вершины параболы y = 2x2- 8x+9.
Ответ: ------------------------------------ .
5. Укажите график функции, заданной формулой у=х2+4х+3.
1) 2)
3) 4)
6. На рисунке изображен график функций вида y = kx+b. Определите знаки коэффициентов k и b.
1) ) k0, bkb0; 3) kbk0, b0.
7. Каждый график соотнесите с соответствующей формулой.
А) y=; В) y=2-x2; С) y=2x; Д) y=2x+2.
1) 2)
3)
4)
| 1) | 2) | 3) | 4) |
|
|
|
|
|
8. Дана функция у=ах2+вх+с. На каком рисунке изображен график этой функции, если известно, что a2+вх+с имеет два положительных корня?
1) 2)
3)
4)
Ответ: -------------------------- .
| 9. На тренировке в 50-метровом бассейне пловец проплыл 200-метровую дистанцию. На рисунке изображен график зависимости расстояния s (в метрах) между пловцом и точкой старта от времени движения t (в секундах) пловца. Определите по графику, за какое время пловец преодолел 130 метров. Ответ: ___________________________________ |
|
10. Какая из точек А (2; 1), В(-2; -1), С(-1; -1), Д(3; ) принадлежит графику функции y = f(x), где f(x) =
1) точка А ; 2) точка В; 3) точка С; 4) точка Д.
11. Найдите с и постройте график функции у = х2 + с, если известно, что прямая у = 4х имеет с этим графиком ровно одну общую точку.
12.Запишите уравнение прямой , проходящей через точки А( - 13; 75) и В (15; - 65). Тест № 7 по теме «Практико ориентированные задачи»
2.Площадь территории России составляет 1,7 км2, а Турции – 7,8
5 км2. Во сколько раз территория России больше территории Турции?
1) примерно в 2,2 раза; 2) примерно в 22 раза; 3) примерно в 220 раз;
4) примерно в 45 раз.
3.На рулоне обоев имеется надпись, гарантирующая, что длина полотна обоев находится в пределах 10±0,05 м. Какую длину не может иметь полотно при этом условии?
1) 10,05 м; 2) 10,04 м; 3) 10,95 м; 4) 10,03 м.
III. Обобщающая тестовая работа в 9 классе.
Часть 1
Найдите значение выражения 0,6∙ (- 10)3 + 50.
Ответ:
Между какими числами заключено число
?
7 и 8
20 и22
58 и 60
3 и 4
Ответ:
Найдите значение выражения
Ответ:
Решите уравнение 3(- 7 – 3х) = 10х – 2.
Ответ:
5. Дана функция у=ах2+вх+с. На каком рисунке изображен график этой функции, если известно, что a0 и квадратный трехчлен ах2+вх+с имеет два положительных корня?
1) 2)
3)
4)
4)
Ответ: -------------------------- .
Геометрическая прогрессия ( bn) задана условием bn = -7
n. Найдите сумму её первых четырёх членов.
Ответ:
Найдите значение выражения
+
)∙
при а = - 7,2.
Ответ:
При каких значениях а выражение 3а + 1 принимает положительные значения?
а
-
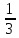
а
- 3
а
а
- 3
Ответ:
Функции заданы формулами:
Y=x2+4
Y=x2
Y= - x2.
Какие из этих функций имеют наименьшее значение?
Ответ:
10.
11. Площадь территории США составляет 9,6 км2, а Молдавии – 3,4
4 км2. Во сколько раз территория США больше территории Молдавии?
1) примерно в 280 раз; 2) примерно в 28 раз; 3) примерно в 2.8 раза;
4) примерно в 35 раз.
Ответ:
12. Городской бюджет составляет 19 млн рублей, а расходы на одну из его статей составили 15%. Сколько рублей потрачено на эту статью бюджета?
Ответ:
13.Выразите из формулы Q = cm(t2 – t1) переменную t1.
Ответ-------------------------------
14.На экзамене 25 билетов, Стас не выучил 5 из них. Найдите вероятность того, что ему попадётся выученный билет.
Ответ:
15.Период колебания математического маятника ( в секундах) приближённо можно вычислить по формуле T=2 , где l – длина нити в метрах. Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 6 секунд.
Ответ:
При выполнении заданий 17 – 19 запишите решение.
17. Решите уравнение х3 = 3х2 + 4х.
18. Первая труба пропускает на 13 литров воды в минуту меньше, чем вторая труба. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 208 литров она заполняет на 8 минут дольше, чем вторая труба?
19.Найдите с и постройте график функции y= x2 + c , если известно, что прямая y= 6x имеет с этим графиком ровно одну общую точку.



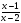 2)
2) 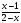 3)
3) 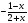 4)
4) 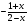
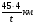 ; 2)
; 2) 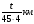 ; 3)
; 3) 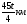 ; 4)
; 4)