
Линейная функция,
её график, свойства.

Укажите линейные уравнения :
1) 5y = x
2) 3y = 0
3) y 2 + 16x 2 = 0
4) + y = 4
5) x + y =4
6) y = -x + 11
7) + 0.5x – 2 = 0
8) 25d – 2m + 1 = 0
9) y = 3 – 2x
5

- Функция вида у = kx + b называется линейной .
- Графиком функции вида у = kx +b является прямая .
- Для построения прямой необходимы только две точки , так как через две точки проходит единственная прямая.

Найти уравнения линейных функций
y=-x+0,2; y=12,4x-5,7 ; y=-9x-18; y=5,04x;
y=-5,04x; y=126,35+8,75x;
y=x-0,2; y=x:8;
y=0,005x; y=133,133133x; y=3-10, 01x; y=2:x;
y=-0,0049; y=х:62.

y = kx + b – линейная функция
х – аргумент (независимая переменная)
у – функция (зависимая переменная)
k, b – числа (коэффициенты)
к ≠ 0

х
Х 1
у
Х 2
У 1
Х 3
У 2
У 3
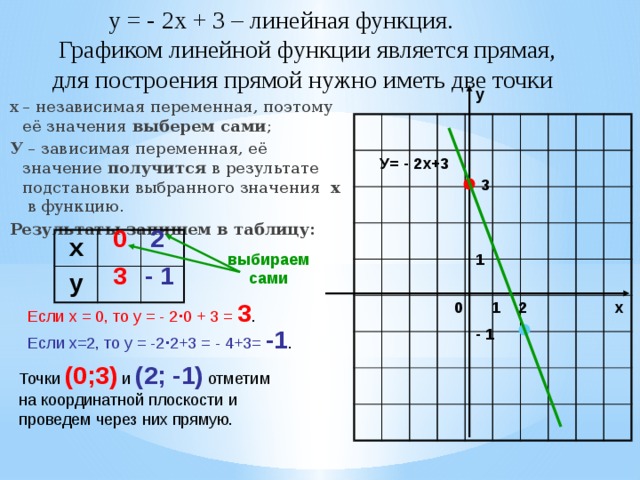
у = - 2х + 3 – линейная функция. Графиком линейной функции является прямая, для построения прямой нужно иметь две точки
у
х – независимая переменная, поэтому её значения выберем сами ;
У – зависимая переменная, её значение получится в результате подстановки выбранного значения х в функцию.
Результаты запишем в таблицу:
У= - 2х+3
3
2
0
х
у
выбираем
1
сами
- 1
3
2
0
1
Если х = 0, то у = - 2 · 0 + 3 = 3 .
х
- 1
Если х=2, то у = -2 · 2+3 = - 4+3= -1 .
Точки (0;3) и (2; -1) отметим
на координатной плоскости и
проведем через них прямую.
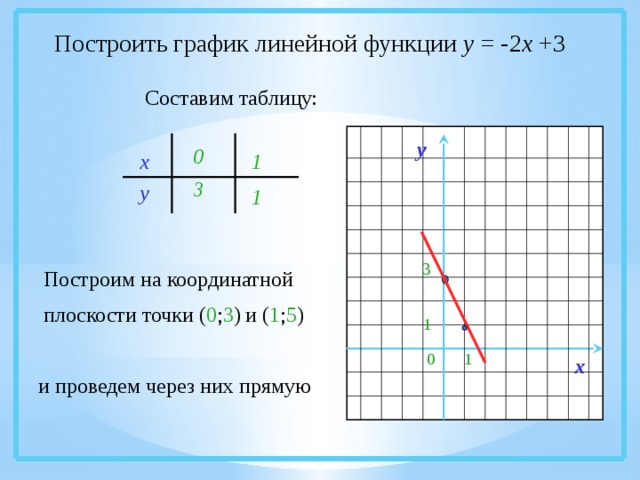
Построить график линейной функции у = -2 х +3
Составим таблицу:
у
03
х
1
у
1
3
Построим на координатной плоскости точки ( 0 ; 3 ) и ( 1 ; 5 )
1
1
0
х
и проведем через них прямую

Построить график линейной функции
I вариант II вариант
y=x-4 y=-x+4
Определить взаимосвязь коэффициентов
k и b и расположения прямых
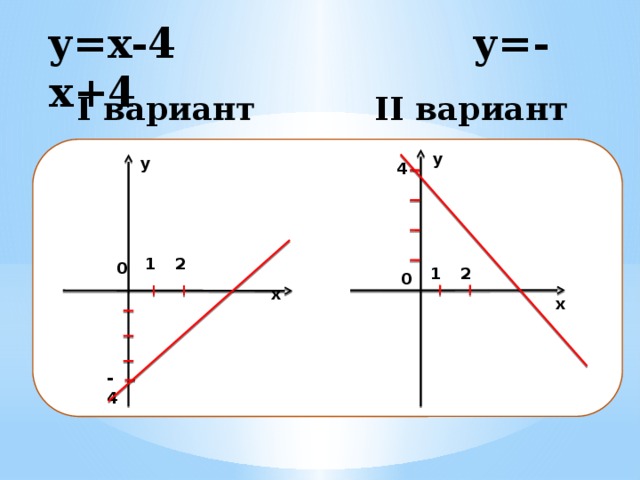
y=x-4 y=-x+4
II вариант
I вариант
y
y
4
2
1
0
1
2
0
x
x
-4
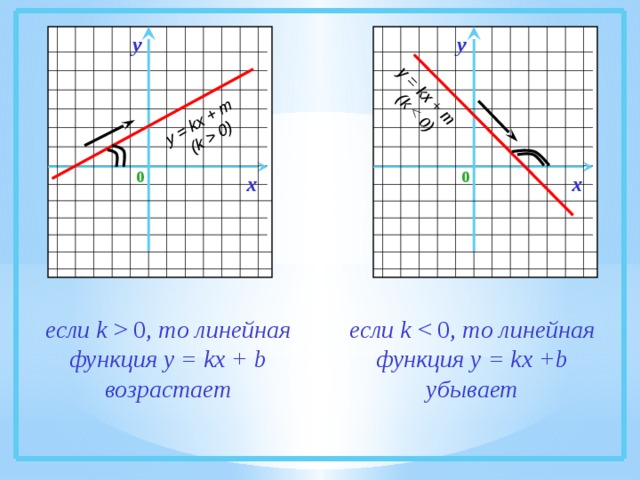 0) у у 0 0 х х если k 0, то линейная функция у = kx + b возрастает если k то линейная функция у = kx +b убывает" width="640"
0) у у 0 0 х х если k 0, то линейная функция у = kx + b возрастает если k то линейная функция у = kx +b убывает" width="640"
y = kx + m
(k
y = kx + m
(k 0)
у
у
0
0
х
х
если k 0, то линейная функция у = kx + b возрастает
если k то линейная функция у = kx +b убывает
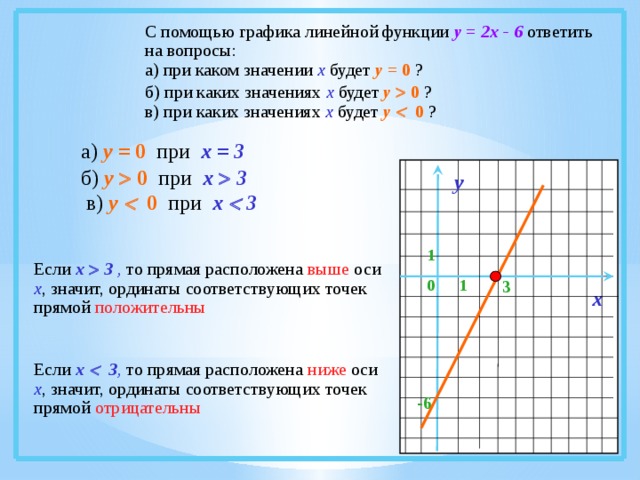
С помощью графика линейной функции у = 2х - 6 ответить на вопросы:
а) при каком значении х будет у = 0 ?
б) при каких значениях х будет у 0 ?
в) при каких значениях х будет у 0 ?
а) у = 0 при х = 3
б) у 0 при х 3
у
в) у 0 при х 3
1
Если х 3 , то прямая расположена выше оси х , значит, ординаты соответствующих точек прямой положительны
3
0
1
х
Если х 3 , то прямая расположена ниже оси х , значит, ординаты соответствующих точек прямой отрицательны
-6

Задания для самостоятельного решения: построить графики функций (выполнять в тетради)
1. у = 2х – 2
3. у = 4 – х
4. у = 1 – 3х
2. у = х + 2
Обратите внимание:
точки, выбранные вами для построения прямой, могут быть другими,
но расположение графиков обязательно должно совпадать
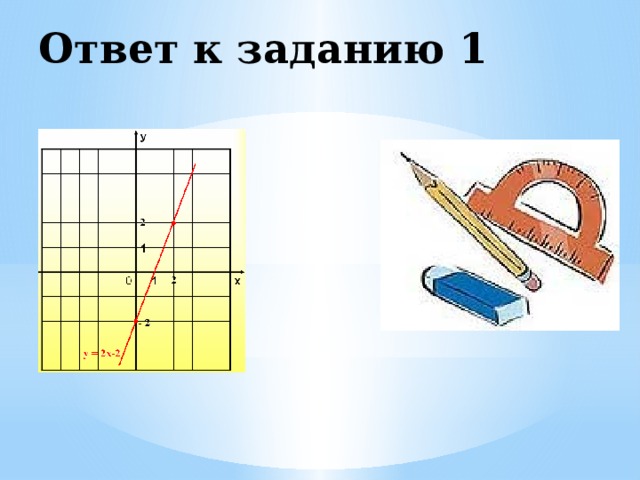
Ответ к заданию 1
12

Ответ к заданию 2
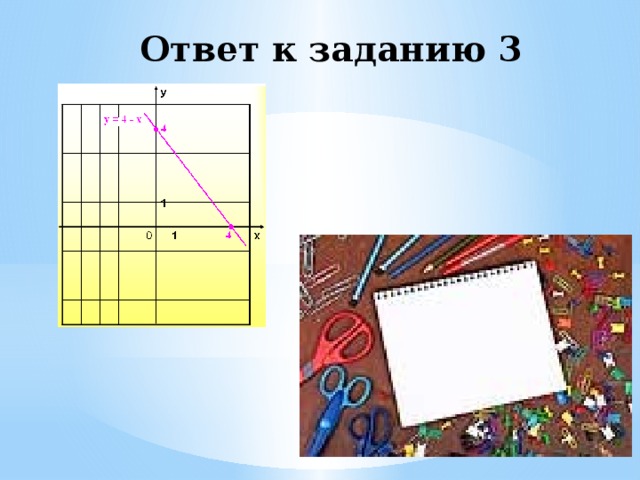
Ответ к заданию 3
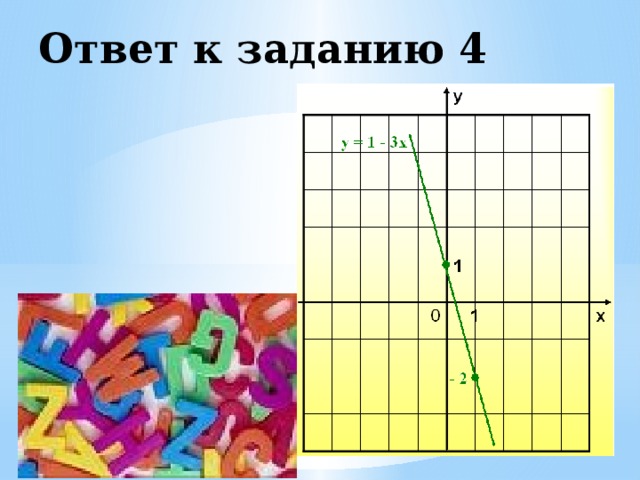
Ответ к заданию 4
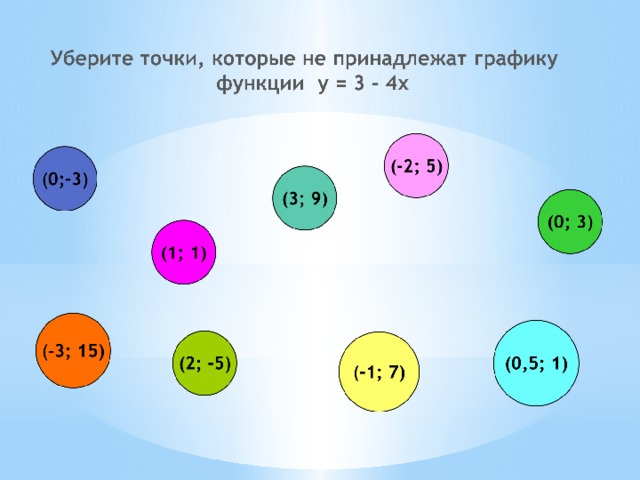
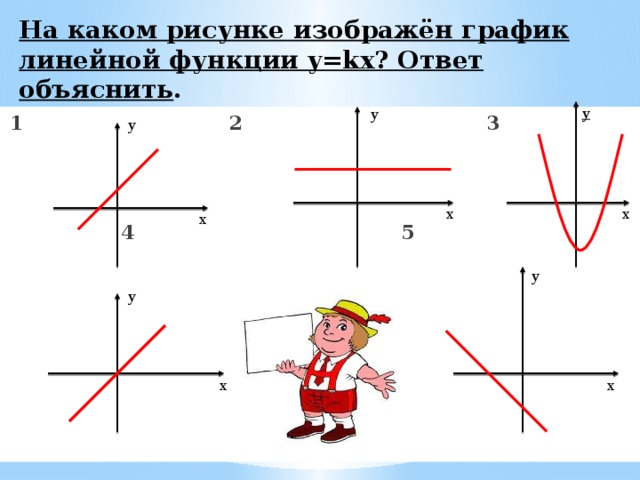
На каком рисунке изображён график линейной функции y=kx? Ответ объяснить .
y
y
1 2 3
4 5
y
x
x
x
y
y
x
x
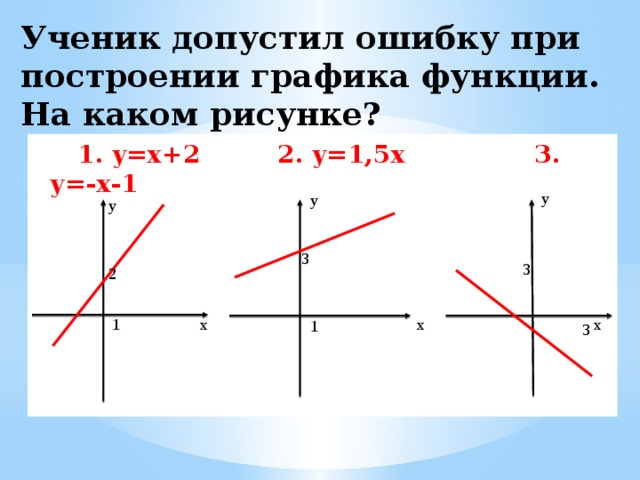
Ученик допустил ошибку при построении графика функции. На каком рисунке?
1. y=х+2 2. y=1,5х 3. y=-х-1
y
y
y
3
3
2
1
x
x
x
1
3

На каком рисунке коэффициент k отрицателен?
1 2 3
4 5
y
y
y
x
x
x
y
y
x
x
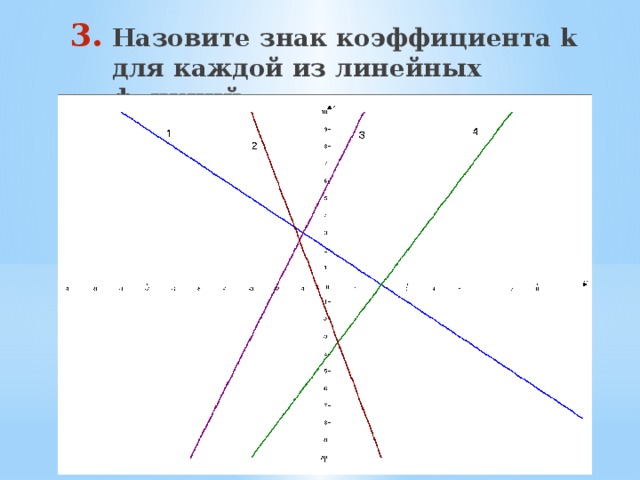
- Назовите знак коэффициента k для каждой из линейных функций:
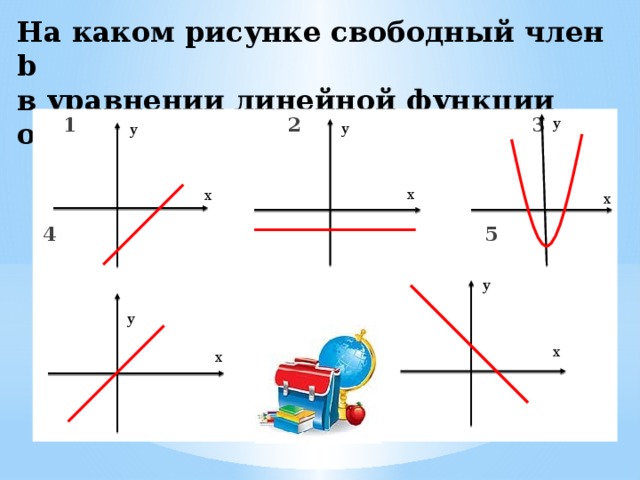
На каком рисунке свободный член b в уравнении линейной функции отрицателен?
y
1 2 3
4 5
y
y
x
х
x
y
y
x
x
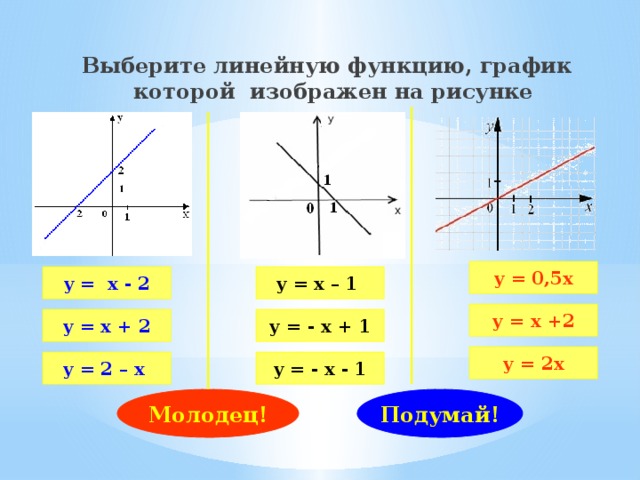
Выберите линейную функцию, график которой изображен на рисунке
у = 0,5х
у = х - 2
у = х – 1
у = х +2
у = х + 2
у = - х + 1
у = 2х
у = 2 – х
у = - х - 1
Молодец!
Подумай!
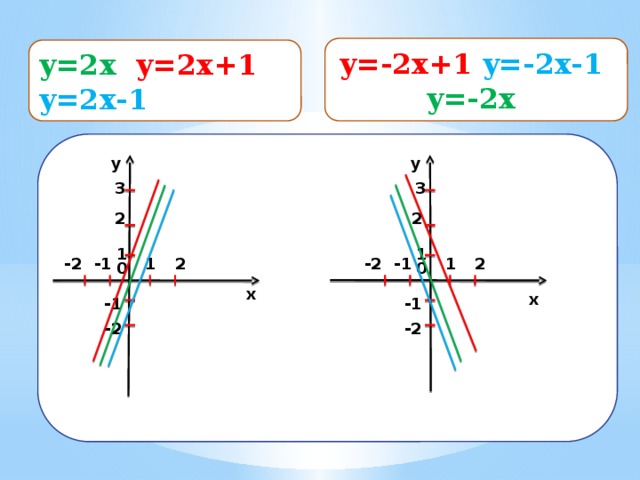
y=-2x+1 y=-2x-1
y=-2x
y=2x y=2x+1 y=2x-1
y
y
3
3
2
2
1
1
2
1
-1
2
1
-2
-1
-2
0
0
x
x
-1
-1
-2
-2
12
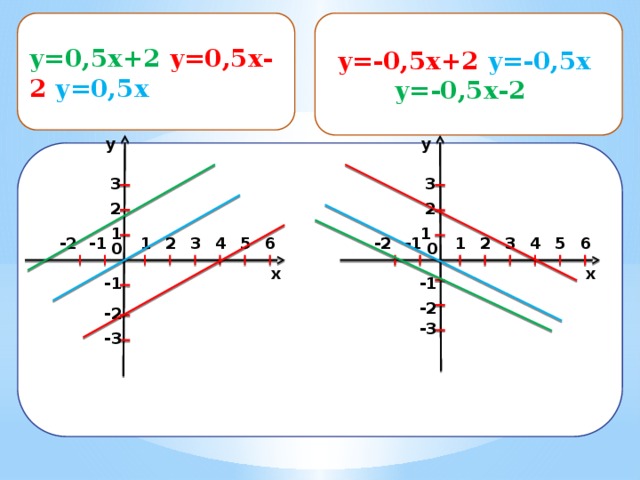
y=0,5x+2 y=0,5x-2 y=0,5x
y=-0,5x+2 y=-0,5x
y=-0,5x-2
y=-0,5x+2, y=-0,5x, y=-0,5x-2
y
y
3
3
2
2
1
1
4
6
1
2
5
3
-2
-1
1
3
6
5
4
2
-2
-1
0
0
x
x
-1
-1
-2
-2
-3
-3
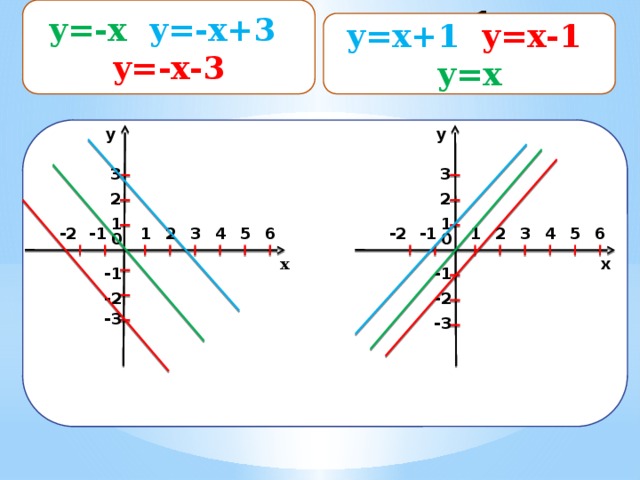
y=-x y=-x+3
y=-x-3
y=x+1 y=x-1 y=x
y=x+1 y=x-1 ,y=x
y
y
3
3
2
2
1
1
-1
1
2
6
5
4
3
1
-2
-1
4
2
-2
5
6
3
0
0
x
x
-1
-1
-2
-2
-3
-3

Составить уравнение
линейной функции по следующим условиям:

подведем
итог

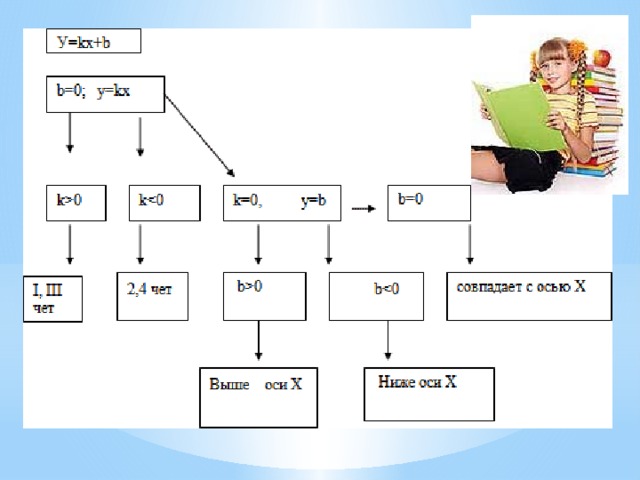
Мы узнали: *Функция вида у = kx + b называется линейной. *Графиком функции вида у = kx + b является прямая. *Для построения прямой необходимы только две точки, так как через две точки проходит единственная прямая. *Коэффициент k показывает возрастает или убывает прямая. *Коэффициент b показывает, в какой точке прямая пересекает ось OY. *Условие параллельности двух прямых.
Выводы записать в тетрадь

Желаю успехов!







