
Урок по теме: Многоугольники
Цели урока:
- Ввести понятие многоугольника и его элементов, научиться определять вид многоугольника, вычислять сумму углов многоугольника.
- Развивать логическое мышление, воспитывать интерес к геометрии, чувство товарищества и взаимопонимания

- Многоуго́льником называется геометрическая фигура, состоящая из n
(n больше или равно 3) точек плоскости , не лежащих на одной прямой и попарно соединённых непересекающимися отрезками
- Многоугольник -это замкнутая ломаная линия.

Какие из фигур являются многоугольниками?
3
1
2
6
4
5
10
8
7
9
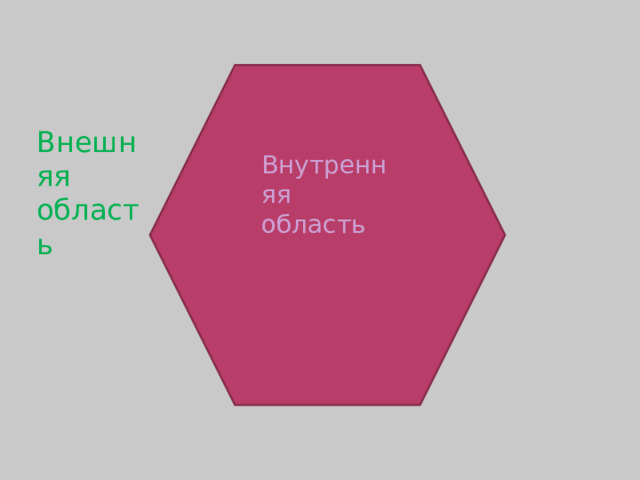
Внешняя область
Внутренняя область
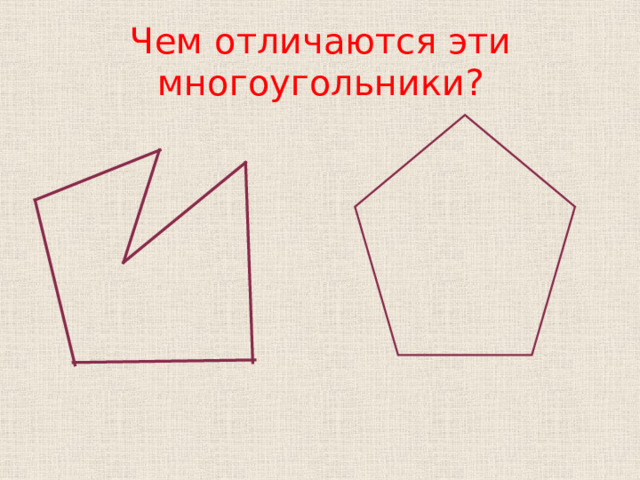
Чем отличаются эти многоугольники?
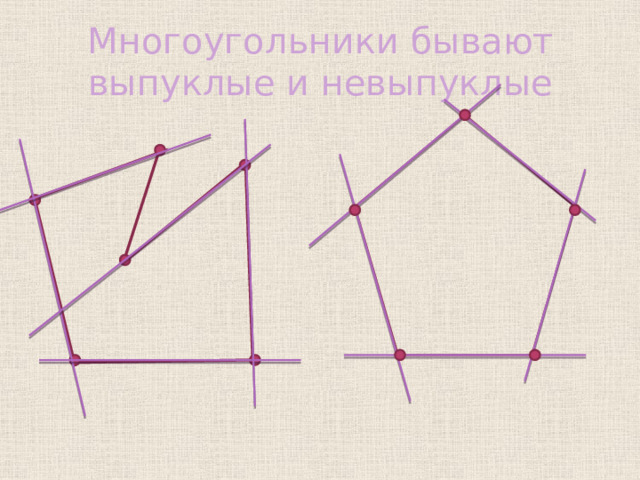
Многоугольники бывают выпуклые и невыпуклые
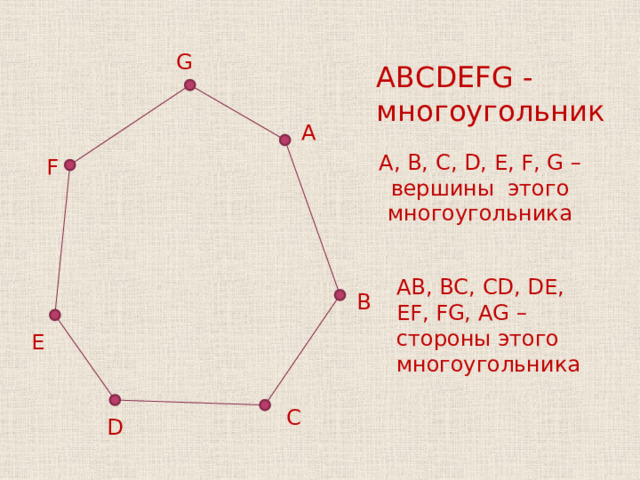
G
ABCDEFG -многоугольник
A
A, B, C, D, E, F, G – вершины этого многоугольника
F
AB, BC, CD, DE, EF, FG, AG – стороны этого многоугольника
B
E
C
D
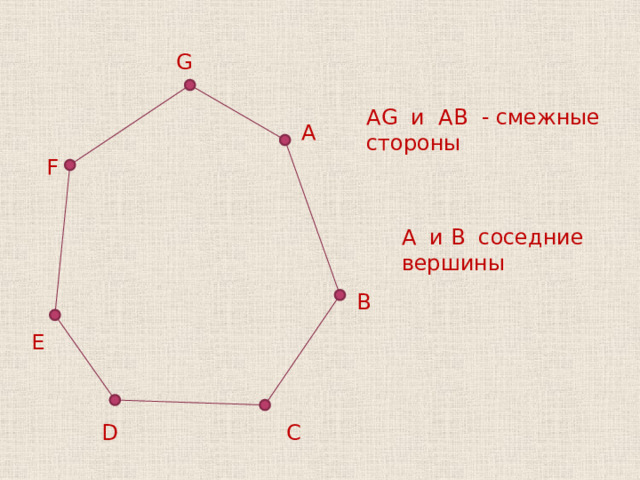
G
AG и AB - смежные стороны
A
F
A и B соседние вершины
B
E
С
D
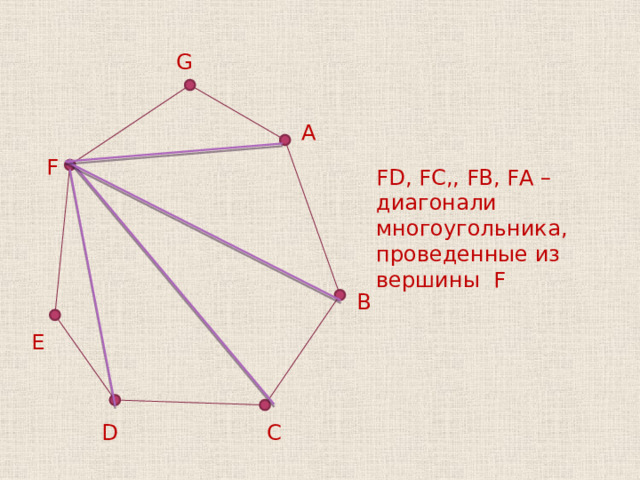
G
A
F
FD, FC,, FB, FA – диагонали многоугольника , проведенные из вершины F
B
E
С
D
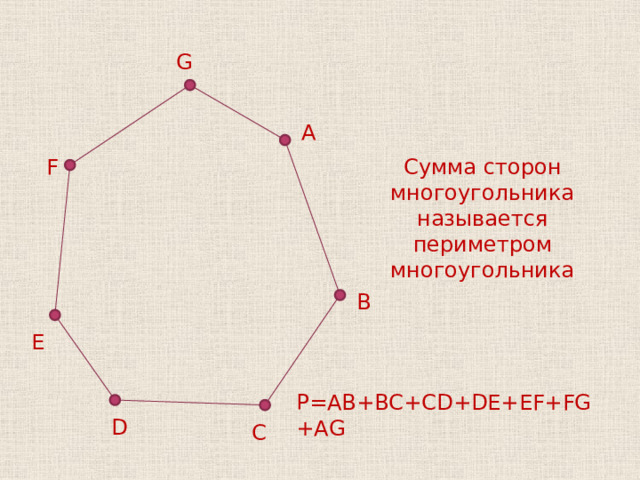
G
A
Сумма сторон многоугольника называется периметром многоугольника
F
B
E
P=AB+BC+CD+DE+EF+FG+AG
D
C
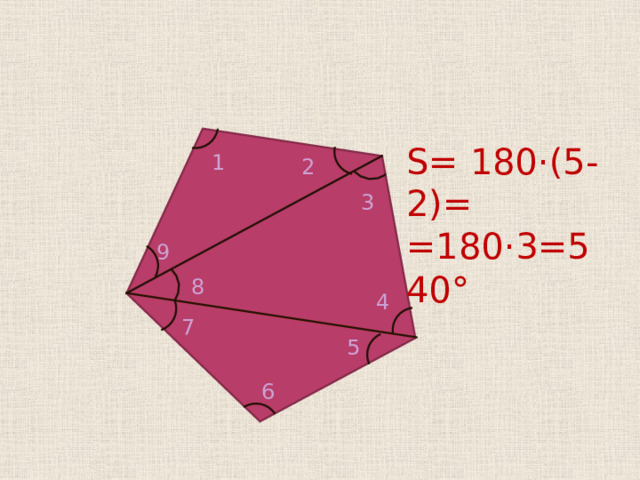
S = 180·(5-2)=
=180·3=540°
1
2
3
9
8
4
7
5
6
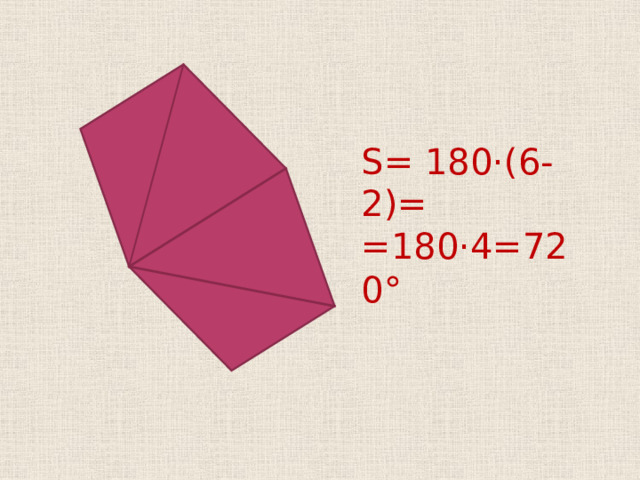
S = 180·(6-2)=
=180·4=720°
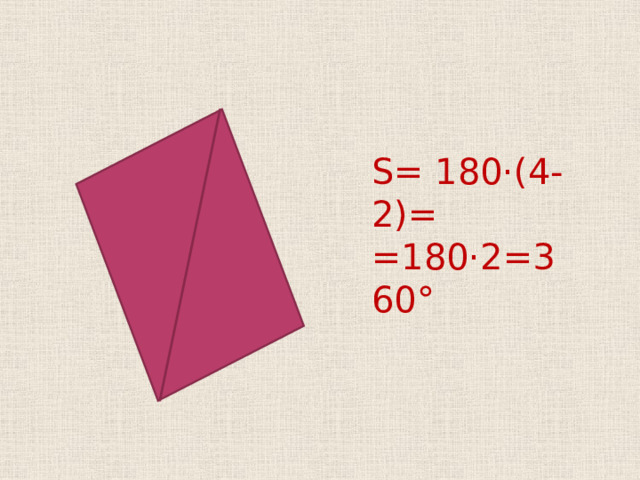
S = 180·(4-2)=
=180·2=360°
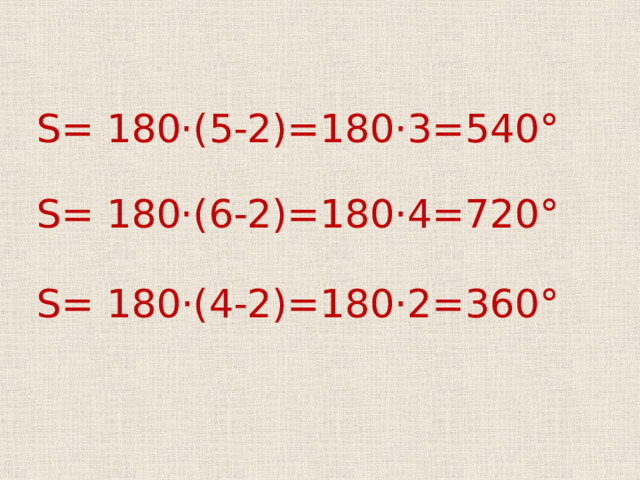
S = 180·(5-2)=180·3=540°
S = 180·(6-2)=180·4=720°
S = 180·(4-2)=180·2=360°

Сумма углов выпуклого n -угольника:
S=180°·(n-2)

№ 365(в). Дано: n-угольник, α=120°, Найти n. Решение: 120n=(n-2)180 120n=180n-360 360=180n-120n 360=60n n=6
Ответ: 6 сторон


Ответы к самостоятельной работе .

Критерии оценок
- За 4 правильных задания - оценка «5»
- За 3 правильных задания – оценка «4»
- За 2 правильных задания – оценка «3»
- Если решено меньше двух заданий, то материал урока усвоен плохо, нужно дома очень постараться

Домашнее задание
- П.39, 40, 41
- № 365(г)
- № 367
- № 369

Спасибо всем!







