Государственное бюджетное общеобразовательное учреждение "Камско-Устьинская кадетская школа-интернат имени Героя Советского Союза Чиркова Михаила Алексеевича"
«Рассмотрено» «Согласовано» «Утверждаю»
На заседании ШМО Зам.Директора по УР Директор КШИ
Протокол №_____ ____________Н.Г.Семагина ____________И.М.Гумеров
От «__»________20__г. «___»_________20__г. «__»________20__г.
Руководитель ШМО
____________О.А.Ларионова
Рабочая программа учебного предмета
«Математика» для 6 класса
«Рассмотрено» Составитель: учитель математики
На педсовете ГБОУ "Камско-Устьинскаякадетская
Протокол № 1 школа-интернат имени Героя
От «29»августа 2017г. Советского Союза Чиркова Михаила
Алексеевича"
Палёнова Светлана Аркадьевна.
2017 – 2018уч.год
РАБОЧАЯ ПРОГРАММА
ДЛЯ ОСНОВНОГО ОБЩЕГО ОБРАЗОВАНИЯ
Структура программы
Программа включает четыре раздела:
Пояснительная записка.
Содержание курса математики 6 класса.
Тематическое планирование с определением основных видов учебной деятельности обучающихся.
Дополнительная литература.
Пояснительная записка.
Рабочая программа математики 6 класса составлена на основе:
Федеральный закон от 29.12.2012 № 273-ФЗ «Об образовании в Российской Федерации»
Федерального государственного образовательного стандарта основного общего образования, утвержденного приказом Министерства образования и науки Российской Федерации 17.12.2010 № 1897 (Далее - ФГОС)
Порядка организации и осуществления образовательной деятельности по основным общеобразовательным программам – образовательным программам начального общего, основного общего и среднего общего образования, утвержденного приказом Министерства образования и науки Российской Федерации от 30.08.2013 г. № 1015;
Федерального перечня учебников, рекомендованных и допущенных к использованию в образовательном процессе в образовательных организациях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию;
СанПиН 2.4.2.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях»;
Постановления Главного государственного санитарного врача РФ «Об утверждении СанПиН 2.4.4.3172-14 «Санитарно-эпидемиологические требования к устройству, содержанию и организации режима работы образовательных организаций дополнительного образования детей»;
Примерной основной образовательной программы основного общего образования;
Закон Республики Татарстан «Об образовании»;
Приказ МО и Н РТ № 4620/11 от 23 сентября 2011 года « Об утверждении примерных учебных планов для кадетских школ, кадетских школ-интернатов и кадетских классов в общеобразовательных учреждениях Республики Татарстан».
Учебный план КШИ им Героя Советского Союза Чиркова М.А. на 2017-2018 уч. год от 28.08.2017 год
Рабочая программа разработана на основе авторской программы Е.А.Бунимович «Математика. Рабочие программы. Предметная линия учебников «Сфера» 5-6 классы»– Москва «Просвещение», 2011 .
В рабочей программе учтены идеи и положения Концепции духовно-нравственного развития и воспитания личности гражданина России. Программы развития и формирования универсальных учебных действий, которые обеспечивают формирование российской гражданской идентичности, овладения ключевыми компетенциями, составляющими основу для саморазвития и непрерывного образования, целостность общекультурного, личностного и познавательного развития учащихся, и коммуникативных качеств личности.
Эта программа является основой для организации работы учителя, ведущего преподавание по указанному учебно-методическому комплекту. В ней цели и требования к результатам обучения математике в основной школе конкретизированы применительно к этапу 5-6 классов. Программа задаёт содержание и структуру курса, последовательность учебных тем в учебниках линии «Сферы». В ней также приводится характеристика видов учебной и познавательной деятельности, которые служат достижению поставленных целей и обеспечиваются УМК «Сферы».
Цели и задачи курса математики
Продолжение формирования центральных математических понятий (число, величина, геометрическая фигура), обеспечивающих преемственность и перспективность математического образования школьников.
Подведение учащихся на доступном для них уровне к осознанию взаимосвязи математики и окружающего мира, понимание математики как части общей культуры человечества.
Развитие интеллектуальных и творческих способностей учащихся, познавательной активности, критичности мышления, интереса к изучению математики.
Формирование умения извлекать информацию, новое знание, работать с учебным математическим текстом.
Вклад математики в достижение целей основного общего образования
Математическое образование играет важную роль, как в практической, так и в духовной жизни общества. Практическая сторона математического образования связана с формированием способов деятельности, духовная — с интеллектуальным развитием человека, формированием характера и общей культуры.
Практическая полезность математики обусловлена тем, что её предметом являются фундаментальные структуры реального мира: пространственные формы и количественные отношения — от простейших, усваиваемых в непосредственном опыте, до достаточно сложных, необходимых для развития научных и технологически идей. Каждому человеку в своей жизни приходится выполнять расчёты, находить в справочниках нужные формулы и применят), и владеть практическими приёмами геометрических измерении и построений, читать информацию, представленную в виде таблиц диаграмм, графиков, понимать вероятностный характер случайных событий, составлять алгоритмы и др.
В школе математика служит опорным предметом для изучения смежных дисциплин. Всё больше специальностей, где пси, ходим высокий уровень образования, связано с непосредственными применением математики (экономика, бизнес, финансы, физика, химия, техника, информатика, биология, психология и др.). Реальной необходимостью в наши дни является
непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической.
В процессе школьной математической деятельности происходит овладение такими мыслительными операциями, как индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Ведущая роль принадлежит математике в формировании алгоритмического мышления и воспитании умений действовать по заданному алгоритму и конструировать новые. В ходе решения задач — основной учебной деятельности на уроках математики — развиваются творческая и прикладная стороны мышления.
Обучение математике дает возможность развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства.
Математическое образование вносит свой вклад в формирование общей культуры человека. Необходимым компонентом культуры в современном толковании является общее знакомство с методами познания действительности, представление о предмете и методе математики, отличиях математического метода от методов естественных и гуманитарных наук, об особенностях применения математики для решения научных и прикладных задач.
История развития математического знания дает возможность пополнить запас историко-научных знаний школьников. Знакомство с основными историческими вехами возникновения и развития математической науки, с историей великих открытий, именами людей, творивших науку, входит в интеллектуальный багаж каждого культурного человека.
Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идеи симметрии.
Общая характеристика курса математики 5-6 классов
В Федеральном государственном образовательном стандарте и Примерной программе основного общего образования сформулированы цели обучения математике в основной школе и требования к результатам освоения содержания курса. Эти целевые установки носят общий характер и задают направленность обучения математике в основной школе в целом. В данной рабочей программе они конкретизированы применительно к этапу 5-6 классов с учетом возрастных возможностей учащихся. В качестве приоритетных выдвигаются следующие цели:
подведение учащихся на доступном для них уровне к осознанию взаимосвязи математики и окружающего мира, пониманию математики как части общей культуры человечества;
развитие познавательной активности; формирование мыслительных операций, являющихся основой интеллектуальной деятельности; развитие логического мышления, алгоритмического мышления; формирование умения точно выразить мысль;
развитие интереса к математике, математических способностей;
формирование знаний и умений, необходимых для изучения курсов математики 7-9 классов, смежных дисциплин, применения в повседневной жизни.
В данной рабочей программе курс 5-6 классов линии УМК «Сферы» представлен как арифметико-геометрический с включением элементов алгебры. Кроме того, к нему отнесено начало изучения вероятностно-статистической линии, а также элементов раздела «Логика и множества», возможность чего предусмотрено Примерной программой по математике для 5 - 9 классов.
Содержание раздела «Арифметика» служит базой для дальнейшего изучения математики и смежных предметов, способствует развитию логического мышления учащихся, формированию умения пользоваться алгоритмами, а также приобретении практических навыков, необходимых в повседневной жизни. При изучении арифметики формирование теоретических знании сочетается с развитием вычислительной культуры, которая актуальна и при наличии вычислительной техники, в частности, г обучением простейшим приёмам прикидки и оценки результата вычислений. Развитие понятия о числе связано с изучением рациональных чисел: натуральных чисел, обыкновенных и десятичных дробей, положительных и отрицательных чисел. Параллельно на доступном для учащихся данного возраста уровне г. курсе представлена научная идея — расширение понятия числа.
В задачи изучения раздела «Геометрия» входит развитие геометрических представлений учащихся, образного мышления, пространственного воображения, изобразительных умений. Этот этап изучения геометрии осуществляется в 5-6 классах на наглядно-практическом уровне, при этом большая роль отводится опыту, эксперименту. Учащиеся знакомятся с геометрическими фигурами и базовыми конфигурациями, овладевают некоторыми приёмами построения, открывают их свойства, применяют эти свойства при решении задач конструктивного и вычислительного характера.
Изучение раздела «Алгебра» в основной школе предполагает, прежде всего, овладение формальным аппаратом буквенного исчисления. Это материал более высокого, нежели арифметика уровня абстракции. Его изучение решает целый ряд задач методологического, мировоззренческого, личностного характера, но в то же время требует определенного уровня интеллектуального развития. Поэтому в курсе 5-6 классов представлены только начальные, базовые алгебраические понятия, и он играет роль своего рода мостика между арифметикой и алгеброй, назначение которого можно образно описать так: от чисел к буквам.
Изучение раздела «Вероятность и статистика» вносит существенный вклад в осознание учащимися прикладного и практического значения математики. В задачи его изучения входит формирование умения воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, оценивать вероятность наступления события. Основное содержание этого раздела отнесено к 7-9 классам. Для курса 5-6 классов выделены следующие вопросы: формирование умений работать с информацией, представленной в форме таблиц и диаграмм, первоначальных знаний о приёмах сбора и представления информации, первое знакомство с комбинаторикой, решение комбинаторных задач.
Введение в курс элементарных теоретико-множественных понятий и соответствующей символики способствует обогащению математического языка школьников, формированию умения точно и сжато формулировать математические предложения, помогает обобщению и систематизации знаний.
В содержание основного общего образования, предусмотренного Примерными программами по математике для 5-9 классов, включён также раздел «Математика в историческом развитии». Его элементы представлены и в содержании курса 5-6 классов. Назначение этого материала состоит в создании гуманитарного, культурно-исторического фона при рассмотрении проблематики основного содержания.
Место математики в учебном плане основной школы
В соответствии с учебным планом основного общего образования в курсе математики выделяются два этапа — 5-6 классы и 7-9 классы, у каждого из которых свои самостоятельные функции. В 5-6 классах изучается интегрированный предмет «Математика», в 7—9 классах — два предмета «Алгебра» и «Геометрия». Курс 5—6 классов, с одной стороны, является непосредственным продолжением курса математики начальной школы, систематизирует, обобщает и развивает полученные там знания, с другой стороны, позволяет учащимся адаптироваться к новому уровню изучения предмета, создает необходимую основу, на которой будут базироваться систематические курсы 7-9 классов.
На изучение математики в основной школе отводится 5 часов в неделю в течение всех лет обучения. Таким образом, на интегрированный курс «Математика» в 5-6 классах всего отводится 350 уроков.
Личностные, метапредметные и предметные результаты освоения конкретного учебного предмета, курса;
К важнейшим результатам обучения математике в 5-6 классах при преподавании по УМК «Сферы» относятся следующие:
• в личностном направлении:
1) знакомство с фактами, иллюстрирующими важные этапы развития математики (изобретение десятичной нумерации, обыкновенных дробей, десятичных дробей; происхождение геометрии из практических потребностей людей);
способность к эмоциональному восприятию математических объектов, рассуждений, решений задач, рассматриваемых проблем;
умение строить речевые конструкции (устные и письмен ные) с использованием изученной терминологии и символики, понимать смысл поставленной задачи, осуществлять перевод с естественного языка на математический и наоборот;
в метапредметном направлении:
умение планировать свою деятельность при решении учебных математических задач, видеть различные стратегии решения задач, осознанно выбирать способ решения;
умение работать с учебным математическим текстом, находить ответы на поставленные вопросы, выделять смысловые фрагменты и пр.);
умение проводить несложные доказательные рассуждения, опираясь на изученные определения, свойства, признаки, распознавать верные и неверные утверждения; иллюстрировать примерами изученные понятия и факты; опровергать с помощью контрпримеров неверные утверждения;
умение действовать в соответствии с предложенным алгоритмом, составлять несложные алгоритмы вычислений и построений;
применение приёмов самоконтроля при решении учебных задам ,
умение видеть математическую задачу в несложных практических ситуациях;
в предметном направлении:
владение базовым понятийным аппаратом по основным разделам содержания;
владение навыками вычислений с натуральными числа ми, обыкновенными и десятичными дробями, положительными и отрицательными числами;
умение решать текстовые задачи арифметическим способом, используя различные стратегии и способы рассуждения;
усвоение на наглядном уровне знаний о свойствах плоских и пространственных фигур; приобретение навыков их изображения; умение использовать геометрический язык для описания предметов окружающего мира;
приобретение опыта измерения длин отрезков, величин углов, вычисления площадей и объёмов; понимание идеи измерения длин, площадей, объёмов;
знакомство с идеями равенства фигур, симметрии; умение распознавать и изображать равные и симметричные фигуры;
умение проводить несложные практические расчеты (включающие вычисления с процентами, выполнение необходимых измерений, использование прикидки и оценки);
использование букв для записи общих утверждений, фор мул, выражений, уравнений; умение оперировать понятием «буквенное выражение», осуществлять элементарную деятельность, связанную с понятием «уравнение»;
знакомство с идеей координат на прямой и на плоскости выполнение стандартных процедур на координатной плоскости:
понимание и использование информации, представленной в форме таблицы, столбчатой или круговой диаграммы;
умение решать простейшие комбинаторные задачи перебором возможных вариантов.
СОДЕРЖАНИЕ КУРСА МАТЕМАТИКИ 5-6 КЛАССОВ
Арифметика
Натуральные числа. Натуральный ряд. Десятичная система счисления. Арифметические действия с натуральными числами. Свойства арифметических действий.
Степень с натуральным показателем.
Числовые выражения, значение числового выражения. Порядок действий в числовых выражениях, использование скобок. Решение текстовых задач арифметическим способом.
Делители и кратные. Свойства и признаки делимости. Простые и составные числа. Разложение натурального числа на простые множители. Деление с остатком.
Дроби. Обыкновенная дробь. Основное свойство дроби. Сравнение обыкновенных дробей. Арифметические действия с обыкновенными дробями. Нахождение части от целого и целого по его части.
Десятичная дробь. Сравнение десятичных дробей. Арифметические действия с десятичными дробями. Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной.
Проценты; нахождение процента от величины и величины по ее проценту. Отношение; выражение отношения в процентах.
Решение текстовых задач арифметическим способом.
Рациональные числа. Положительные и отрицательные числа, модуль числа. Множество целых чисел. Множество рациональных чисел; рациональное число как отношение  , где т — целое число, п — натуральное. Сравнение рациональных чисел. Арифметические действия с рациональными числами. Свойства арифметических действий.
, где т — целое число, п — натуральное. Сравнение рациональных чисел. Арифметические действия с рациональными числами. Свойства арифметических действий.
Координатная прямая; изображение чисел точками координатной прямой.
Измерения, приближения, оценки. Единицы измерения длины, площади, объёма, массы, времени, скорости. Приближённое значение величины. Округление натуральных чисел и десятичных дробей. Прикидка и оценка результатов вычислений.
Элементы алгебры
Использование букв для обозначения чисел, для записи свойств арифметических действий. Буквенные выражения. Числовое значение буквенного выражения. Допустимые значения букв в выражении.
неизвестных компонентов арифметических действий. Примеры решения текстовых задач с помощью уравнений.
Декартовы координаты на плоскости. Построение точки по координатам, определение координат точки на плоскости.
Описательная статистика. Комбинаторика
Представление данных в виде таблиц, диаграмм.
Решение комбинаторных задач перебором вариантов.
Наглядная геометрия
Наглядные представления о фигурах на плоскости: прямая, отрезок, луч, угол, ломаная, многоугольник, окружность, круг, четырёхугольник, прямоугольник, квадрат. Треугольник, видь треугольников. Правильные многоугольники. Изображение геометрических фигур. Взаимное расположение двух прямых, двух окружностей, прямой и окружности.
Длина отрезка, ломаной. Периметр многоугольника. Единицы измерения длины. Измерение длины отрезка, построение от резка заданной длины.
Виды углов. Градусная мера угла. Измерение и построение углов с помощью транспортира. Биссектриса угла.
Понятие площади фигуры; единицы измерения площади Площадь прямоугольника, квадрата. Приближённое измерение площади фигур на клетчатой бумаге. Равновеликие фигуры.
Наглядные представления о пространственных фигурах: куб параллелепипед, призма, пирамида, шар, сфера, конус, цилиндр. Изображение пространственных фигур. Примеры сечений. Многогранники. Правильные многогранники. Примерь развёрток многогранников, цилиндра и конуса.
Понятие объёма; единицы объёма. Объём прямоугольного параллелепипеда, куба.
Понятие о равенстве фигур. Центральная, осевая и зеркальная симметрии. Изображение симметричных фигур.
Логика и множества
Множество, элемент множества. Задание множества перечислением элементов, характеристическим свойством. Стандартные обозначения числовых множеств. Пустое множество и его обозначения. Подмножество. Объединение и пересечение множеств.
Иллюстрация отношений между множествами с помощью диаграмм Эйлера-Венна. Пример и контрпример.
Содержание учебного предмета .
6 класс (175 ч.)
Делимость чисел (16 ч)
Делители и кратные числа; наибольший общий делитель и наименьшее общее кратное. Простые и составные числа. Разложение числа на простые множители. Делимость суммы и произведения. Признаки делимости на 2, 5, 10, 3, 9. Деление с остатком; разбиение натуральных чисел на классы по остаткам от деления.
Основная цель - познакомить учащихся с простейшими понятиями теории делимости.
Треугольники и четырехугольники (8 ч)
Треугольники и их виды. Прямоугольник, квадрат. Равенство фигур. Площадь прямоугольника, единицы площади.
Основные цели - познакомить учащихся с классификацией треугольников по сторонам и углам, свойствами прямоугольника и его диагоналей, научить строить прямоугольник на нелинованной бумаге, сформировать понятие равенства фигур, продолжить формирование метрических представлений.
Дроби (13 ч)
Представление о дроби как способе записи части величины. Правильные и неправильные дроби. Изображение дробей точками на координатной прямой. Основное свойство дроби. Сокращение дробей. Приведение дроби к новому знаменателю. Сравнение дробей. Запись натурального числа в виде дроби.
Основные цели - сформировать у учащихся понятия дроби, познакомить с основным свойством дроби и применением его для преобразования дробей, научить сравнивать дроби.
Действия с дробями (34 ч)
Сложение и вычитание дробей. Смешанная дробь; представление смешанной дроби в виде неправильной и выделение целой части числа из неправильной дроби. Умножение и деление дробей; взаимно-обратные дроби. Нахождение части целого и целого по его части. Решение задач арифметическим способом.
Основная цель - выработать прочные навыки выполнения арифметических действий с обыкновенными дробями.
Таблицы и диаграммы (9 ч)
Чтение таблиц с двумя входами. Использование в таблицах специальных символов и обозначений. Столбчатые диаграммы. Простейшие приемы сбора и представления информации.
Основная цель - сформировать умение извлекать информацию из несложных таблиц и столбчатых диаграмм.
Прямые на плоскости и в пространстве (7 ч)
Пересекающиеся прямые. Вертикальные углы, их свойство. Параллельные прямые. Построение параллельных и перпендикулярных прямых. Примеры параллельных и перпендикулярных прямых в окружающем мире. Расстояние между двумя точками, от точки до прямой, между двумя параллельными прямыми, от точки до плоскости.
Основные цели - создать у учащихся зрительные образы всех основных конфигураций, связанных с взаимным расположением двух прямых на плоскости и в пространстве, сформировать навыки построения параллельных и перпендикулярных прямых, научить находить расстояние от точки до прямой, между двумя параллельными прямыми.
Отношения и проценты (17 ч)
Отношение чисел и величин. Масштаб. Деление в данном отношении.
Выражение процентов десятичными дробями; решение задач на проценты. Выражение отношения величин в процентах.
Основные цели - познакомить с понятием "отношение" и сформировать навыки использования соответствующей терминологии; развить навыки вычисления с процентами.
Симметрия (8 ч)
Осевая симметрия. Ось симметрии фигуры. Центральная симметрия. Построение фигуры, симметричной данной относительно прямой и относительно точки. Симметрия в окружающем мире.
Основные цели - познакомить учащихся с основными видами симметрии на плоскости; научить строить фигуру, симметричную данной фигуре относительно прямой, а также точку, симметричную данной относительно точки; дать представление о симметрии в окружающем мире.
Целые числа (13 ч)
Числа, противоположные натуральным. "Ряд" целых чисел. Изображение целых чисел точками на координатной прямой. Сравнение целых чисел. Сложение и вычитание целых чисел; выполнимость операции вычитания. Умножение и деление целых чисел; правила знаков.
Основные цели - мотивировать введение отрицательных чисел; сформировать умение сравнивать целые числа с опорой на координатную прямую, а также выполнять действия с целыми числами.
Рациональные числа (18 ч)
Отрицательные дробные числа. Понятие рационального числа. Изображение чисел точками на координатной прямой. Противоположные числа. Модуль числа, геометрическая интерпретация модуля. Сравнение рациональных чисел. Арифметические действия с рациональными числами, свойства арифметических действий.
Примеры использования координат в реальной практике. Прямоугольная система координат на плоскости. Координаты точки на плоскости, абсцисса и ордината. Построение точек и фигур на координатной плоскости.
Основные цели - выработать навыки действий с положительными и отрицательными числами; сформировать представление о декартовой системе координат на плоскости.
Уравнения. (14 ч)
Раскрывать скобки. Приводить подобные слагаемые. Применять свойства уравнения для нахождения его решения.
Множества. Комбинаторика. (8 ч)
Понятие множества. Примеры конечных и бесконечных множеств. Подмножества. Основные числовые множества и соотношения между ними. Разбиение множества. Объединение и пересечение множеств. Иллюстрация отношений между множествами с помощью кругов Эйлера.
Решение комбинаторных задач перебором всех возможных вариантов.
Случайное событие. Достоверное и невозможное события. Сравнение шансов событий.
Основные цели - познакомить с простейшими теоретико-множественными понятиями, а также сформировать первоначальные навыки использования теоретико-множественного языка; развить навыки решения комбинаторных задач путем перебора всех возможных вариантов.
Повторение курса (10 ч)
Планируемые результаты изучения учебного предмета, курса.
В результате изучения математики ученик будет
знать/понимать
в личностном направлении:
1) знакомство с фактами, иллюстрирующими важные этапы развития математики (изобретение десятичной нумерации, обыкновенных дробей, десятичных дробей; происхождение геометрии из практических потребностей людей);
способность к эмоциональному восприятию математических объектов, рассуждений, решений задач, рассматриваемых проблем;
умение строить речевые конструкции (устные и письменные) с использованием изученной терминологии и символики, понимать смысл поставленной задачи, осуществлять перевод с естественного языка на математический и наоборот;
в метапредметном направлении:
особенности десятичной системы счисления;
названия рядов и классов;
термины «приближённое значение с недостатком», «приближённое значение с избытком»; «степень числа», «основание степени», «показатель степени»
как связаны между собой действия сложения и вычитания, умножения и деления;
переместительное и сочетательное свойства сложения и умножения, распределительное свойство умножения относительно сложения;
что такое «делитель», «кратное», взаимосвязь между ними;
обозначения НОД(а;в) и НОК (а;в);
определение простого числа;
признаки делимости на 2, на 5, на 10, на 3 и на 9;
что означают знаменатель и числитель дроби;
правила сложения, вычитания, умножения и деления дробей с одинаковыми и разными знаменателями;
уметь в предметном направлении:
различать виды линий и углов;
проводить и обозначать прямую, луч, отрезок, ломаную;
строить отрезок заданной длины, угол заданной величины, биссектрису угла; равнобедренный треугольник по боковым сторонам и углу между ними, прямоугольник на нелинованной бумаге с помощью чертёжных инструментов; находить длину отрезка и величину угла;
распознавать окружность, многоугольники, цилиндр, конус, шар, многогранники; проводить окружность заданного радиуса; изображать многоугольники с заданными свойствами, вычислять периметр многоугольника;
переходить от одних единиц измерения к другим единицам, выбирать подходящие единицы измерения в зависимости от контекста задачи;
представлять натуральное число в виде суммы разрядных слагаемых:
читать и записывать натуральные числа, а также числа, записанные римскими цифрами;
сравнивать и упорядочивать натуральные числа и дроби; читать и записывать двойные неравенства;
изображать натуральные числа на координатной прямой;
округлять натуральные числа до указанного разряда, поясняя при этом свои действия;
выполнять арифметические действия с натуральными числами, находить значения числовых выражений, устанавливая порядок выполнения действий;
находить неизвестное число в равенстве на основе зависимости между компонентами действий;
возводить натуральное число в натуральную степень;
решать несложные текстовые задачи арифметическим методом; решать несложные арифметические задачи на движение; на части и уравнивание;
представлять произведение нескольких равных множителей в виде степени с натуральным показателем;
использовать свойства сложения и умножения для преобразования числовых выражений;
находить НОК и НОД;
находить дробь от величины;
соотносить дроби и точки на координатной плоскости;
сокращать дроби, приводить к новому знаменателю, к общему знаменателю;
выделять целую часть из неправильной дроби и представлять смешанное число в виде неправильной дроби;
анализировать готовые таблицы и диаграммы;
заполнять несложные таблицы, следуя инструкции.
| раздел | Планируемые результаты | ||
| личностные | метапредметные | предметные | |
| Арифметика | Ученик получит возможность: Ответственно относится к учебе, Грамотно излагать свои мысли Критично мыслить, быть инициативным, находчивым, активным при решении математических задач. | Ученик научится: Действовать по алгоритму, Видеть математическую задачу в окружающей жизни. Представлять информацию в различных моделях Ученик получит возможность:
Устанавливать причинно-следственные связи. Строить логические рассуждения, Умозаключения и делать выводы Развить компетентность в области использования информационно- коммуникативных технологий. | Ученик научится: •понимать особенности десятичной системы счисления; Формулировать и применять при вычислениях свойства действия над рациональными ( неотриц.) числами4 Решать текстовые задачи с рациональными числами; Выражать свои мысли с использованием математического языка. Ученик получит возможность: Углубить и развить представления о натуральных числах; Использовать приемы рационализирующие вычисления и решение задач с рациональными (неотр) числами. |
| Элементы алгебры. | Ученик получит возможность: Ответственно относится к учебе. Грамотно излагать свои мысли Контролировать процесс и результат учебной деятельности Освоить национальные ценности, традиции и культуру родного края используя краеведческий материал. | Ученик научится: Действовать по алгоритму; видеть математическую задачу в различных формах. Ученик получит возможность: Выделять альтернативные способы достижения цели и выбирать эффективные способы решения. | Ученик научится: Читать и записывать буквенные выражения, составлять буквенные выражения. Составлять уравнения по условию. Решать простейшие уравнения. Ученик получит возможность: Развить представления о буквенных выражениях Овладеть специальными приемами решения уравнений, как текстовых, так и практических задач. |
| Описательная статистика. Комбинаторные задачи | Ученик получит возможность : ответственно относится к учебе, контролировать процесс и результат учебной и математической деятельности. Критично мыслить, быть инициативным, находчивым, активным при решении комбинаторных задач. | Ученик научится: Представлять информацию в различных моделях. Ученик получит возможность: Выделять альтернативные способы достижения цели и выбирать эффективные способы решения | Ученик научится: Решать комбинаторные задачи с помощью перебора вариантов.
Ученик получит возможность: Приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения; Осуществлять их анализ, представлять результаты опроса в виде таблицы. •научится некоторым приемам решения комбинаторных задач. |
| Наглядная геометрия | Ученик получит возможность : ответственно относится к учебе, контролировать процесс и результат учебной и математической деятельности. Критично мыслить, быть инициативным, находчивым, активным при решении геометрических задач. | Ученик научится: действовать по алгоритму, видеть геометрическую задачу в окружающей жизни, представлять информацию в различных моделях. Ученик получит возможность: Извлекать необходимую информацию, анализировать ее, точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификации, логические обоснования.
| Ученик научится: изображать фигуры на плоскости; • использовать геометрический «язык» для описания предметов окружающего мира; • измерять длины отрезков, величины углов, вычислять площади и объёмы фигур; • распознавать и изображать равные и симметричные фигуры; • проводить не сложные практические вычисления.
Ученик получит возможность: углубить и развить представления о геометрических фигурах. |
| Логика и множества | Ученик получит возможность : ответственно относится к учебе, контролировать процесс и результат учебной и математической деятельности. Обсуждать соотношение между основными числовыми множествами. Записывать на символическом языке соотношения между множествами и приводить примеры различных вариантов их перевода на русский язык | Ученик научится: . Исследовать вопрос о числе подмножеств конечного множества Ученик получит возможность : Проводить логические рассуждения по сюжетам текстовых задач с помощью кругов Эйлера. Приводить примеры классификаций из математики и из других областей знания | Ученик научится: Формулировать определения объединения и пересечения множеств. Иллюстрировать эти понятия с помощью кругов Эйлера.
Ученик получит возможность : Использовать схемы в качестве наглядной основы для разбиения множества на непересекающиеся подмножества. |
Критерии и нормы оценки знаний, умений и навыков учащихся.
Оценка письменных контрольных работ обучающихся по математике
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
Учебно- тематический план 6 класс 175 часов, в неделю 5 часов
| № п\п | Разделы, темы | Количество часов | Контрольные работы |
| 1. | Количество тем | 12 |
|
| 2. | Объем часов на прохождение всех тем | 175 |
|
| 3. | Объем часов на прохождение каждой темы |
|
|
| 3.1 | Делимость чисел. | 16 | 1 |
| 3.2 | Треугольники и четырехугольники. | 8 | 1 |
| 3.3 | Дроби. | 13 | 1 |
| 3.4 | Действия с дробями. | 34 | 1 |
| 3.5 | Таблицы и диаграммы. | 9 | 1 |
| 3.6 | Прямые на плоскости и в пространстве. | 7 |
|
| 3.7 | Отношения и проценты. | 17 | 1 |
| 3.8 | Симметрия. | 8 | 1 |
| 3.9 | Целые число. | 13 | 1 |
| 3.10 | Рациональные числа. | 18 | 1 |
| 3.11 | Уравнения. | 14 | 2 |
| 3.12 | Множества. комбинаторика | 8 |
|
| 4. | Повторение курса | 10 | 1 |
| 5. | Контрольные работы | 12 | 12 |
ПОУРОЧНОЕ ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ 6 класс
5 ч в неделю. Всего за год обучения 175 ч.
| № п/п | Темы, входящие в разделы примерной программы | Количество часов. | Основное содержание по темам | Характеристика основных видов деятельности ученика (на уровне учебных действий) | Дата проведения | |
| По плану | Фактически | |||||
| Глава 6. Делимость чисел (16 уроков) Б5 | ||||||
| 1 | Делители и кратные | 3 | Уроки 1-3. Делители и кратные (п. 20) Делители числа. Кратные числа Ресурсы уроков. Учебник: теория, с. 94, 95, упр. № 309-328, исследование — № 329; Задачник-тренажёр: № 205-208, 209-211, 218, 212-214, 221; 215-217, 219; исследование — № 220; Тетрадь-тренажёр: № 129, 133, 134-136 | Формулировать определения понятий «делитель» и «кратное» числа, употреблять их в речи. Находить наибольший общий делитель и наименьшее общее кратное двух чисел, использовать соответствующие обозначения. Решать текстовые задачи, связанные с делимостью чисел | | |
| 2 | | | ||||
| 3 | | | ||||
| 4 | Простые и составные числа. Разложение натурального числа на простые множители | 3 | Уроки 4-6. Простые и составные числа (п. 21) Числа простые, составные и число 1. Решето Эратосфена. Ресурсы уроков. Учебник: теория, с. 98, 99, упр. № 330-336, 338-348, исследование — № 337, 349; Задачник-тренажер№ 222-227. 228 - 230: Тетрадь-тренажёр: № 130, 131; исследование — № 139, 141 | Формулировать определения простого и составного числа, приводить примеры простых и составных чисел. Выполнять разложение числа на простые множители. Использовать математическую терминологию в рассуждениях для объяснения. Находить простые числа, воспользовавшись «решетом Эратосфена» по предложенному в учебнике плану. Выяснять, является ли число составным. Использовать таблицу простых чисел. Проводить несложные исследования, опираясь на числовые эксперименты (в том числе с помощью компьютера) | | |
| 5 | | | ||||
| 6 | | | ||||
| 7 | Свойства делимости. Пример и контрпример | 2 | Уроки 7-8. Делимость суммы и произведения (п. 22) Делимость произведения. Делимость суммы. Контрпример. Ресурсы уроков. Учебник: теория, с. 102, 103, упр. № 350-369, исследование — № 370 | Формулировать свойства делимости суммы и произведения, доказывать утверждения, обращаясь к соответствующим формулировкам. Конструировать математические утверждения с помощью связки «если..., то ...». Использовать термин «контрпример», опровергать утверждение общего характера с помощью контрпримера | | |
| 8 | | | ||||
| 9 | Признаки делимости | 3 | Уроки 9-11. Признаки делимости (п. 23). Признаки делимости на 10, на 5 и на 2. Признаки делимости на 9 и на 3. Ресурсы уроков. Учебник: теория, с. 106, 107, упр. № 371-384, исследование — № 385, 386; Задачник-тренажёр: № 241, 242, 246, 231-237; исследование — № 238, 239, 243-245; Тетрадь- тренажер: № 132, 137 | Формулировать признаки делимости на 2, на 5, на 10, на 3, на 9. Приводить примеры чисел, делящихся и не делящихся на какое-либо из указанных чисел, давать развёрнутые пояснения. Конструировать математические утверждения с помощью связки «если..., то ...», объединять два утверждения в одно, используя словосочетание «в том и только том случае». Применять признаки делимости. Использовать признаки делимости в рассуждениях. Объяснять, верно или неверно утверждение | | |
| 10 | | | ||||
| 11 | | | ||||
| 12 | Деление с остатком | 3 | Уроки 12- 14. Деление с остатком (п. 24) Примеры деления чисел с остатком. Остатки от деления. Ресурсы уроков. Учебник: теория, с. 110, 111, упр. № 387-394, 399-402, исследование № 395 -398, 403; Тетрадь-тренажёр: №138; исследование № 140, 142 | Выполнять деление с остатком при решении текстовых задач и интерпретировать ответ в соответствии с поставленным вопросом. Классифицировать натуральные числа (чётные и нечётные, по остаткам от деления на 3, на 5 и т.п.) | | |
| 13 | | | ||||
| 14 | | | ||||
| 15 | Обобщение и систематизация знаний. | 1 | Уроки 15-16. Обобщение и систематизация знаний. Контроль Ресурсы уроков. Учебник: «Подведём итоги», с. 114; Тетрадь-тренажёр: «Выполняем тест», с. 61; Тетрадь -экзаменатор: Проверочные работы № 1, № 2, с. 30-35; Задачник-тренажёр: Дополнительные вопросы, «Чётно или нечётно», с. 80-82 | Применять понятия, связанные с делимостью натуральных чисел. Использовать свойства и признаки делимости. Доказывать и опровергать с помощью контрпримеров утверждения о делимости чисел. Решать задачи на деление с остатком | | |
| 16 | Контрольная работа №1 по теме "Делимость чисел" | 1 | | | ||
| Глава 7. Треугольники и четырехугольники .(8 уроков) Б5 | ||||||
| 17 | Треугольники. Виды треугольников. Равнобедренный, равносторонний треугольники | 2 | Уроки 17-18. Треугольники и их виды (п. 25) .Классификация треугольников по сторонам. Равнобедренный треугольник. Классификация треугольников по углам. Ресурсы уроков. Учебник: теория, с. 116, 117, упр. № 404-414, 416-418, исследование — № 415; Тетрадь-тренажёр: № 143, 147, 148, 165, 168, 176, 177; исследование — № 167, 169 173 | Распознавать треугольники на чертежах и рисунках приводить примеры аналогов этих фигур в окружающем мире. Изображать треугольники от руки и с использованием чертёжных инструментов, на нелинованной и клетчатой бумаге; моделировать, используя бумагу, проволоку и др. Исследовать свойства треугольников путём эксперимента, наблюдения, измерения, моделирования, в том числе, с использованием компьютерных программ. Измерять длины сторон, величины углов треугольников. Классифицировать треугольники по углам, по сторонам. Распознавать равнобедренные и равносторонние треугольники. Использовать терминологию, связанную с треугольниками. Выдвигать гипотезы о свойствах равнобедренных, равносторонних треугольников, обосновывать их. Объяснять на примерах, опровергать с помощью контрпримеров утверждения о свойствах треугольников. Находить периметр треугольников, в том числе, выполняя необходимые измерения. Конструировать орнаменты и паркеты, изображая их от руки, с помощью инструментов, а также используя компьютерные программы | | |
| 18 | | | ||||
| 19 | Четырехугольник, прямоугольник, квадрат. Изображение геометрических фигур | | Уроки 19 Прямоугольники (п. 26) Прямоугольник. Квадрат. Построение прямоугольника. Периметр прямоугольника. Диагонали прямоугольника. Ресурсы уроков. Учебник: теория, с. 120, 121, упр. № 419-432; Тетрадь- тренажёр: № 149-151, 175; исследование — № 163 | Понятие площади фигуры; единицы измерения площади. Площадь прямоугольника, квадрата. Приближённое измерение площади фигуры на клетчатой бумаге | | |
| 20 | Понятие о равенстве фигур. Изображение геометрических фигур | | Уроки 20-21. Равенство фигур (п. 27) Равные фигуры. Признаки равенства. Ресурсы уроков. Ресурсы уроков. Учебник: теория, с. 124, 125, упр. № 433-446; Тетрадь- тренажёр: №152, 153, 174; исследование — № 161, 162 | Распознавать равные фигуры, проверять равенство фигур наложением. Изображать равные фигуры. Разбивать фигуры на равные части, складывать фигуры из равных частей. Обосновывать, объяснять на примерах, опровергать с помощью контрпримеров утверждения о равенстве фигур. Формулировать признаки равенства отрезков, углов, прямоугольников, окружностей. Конструировать орнаменты и паркеты, изображая их от руки, с помощью инструментов, а также используя компьютерные | | |
| | | |||||
| 21 | | | ||||
| 22 | Понятие площади фигуры; единицы измерения площади. Площадь прямоугольника, квадрата. Приближённое измерение площади фигуры на клетчатой бумаге | | Уроки 22. Площадь прямоугольника (п. 28). Площадь фигуры. Площадь прямоугольника. Площадь арены цирка Ресурсы уроков. Учебник: теория, с. 128, 129, упр. № 447-461, исследование — № 462; Тетрадь-тренажёр: № 146, 154-159; исследование — № 164-166 | Находить приближённое значение площади фигур, разбивая их на единичные квадраты. Сравнивать фигуры по площади и периметру. Решать задачи на нахождение периметров и площадей квадратов и прямоугольников. Выделять в условии задачи данные, необходимые для её решения, строить логическую цепочку рассуждений, сопоставлять полученный результат с условием задачи | | |
| 23 | Обобщение и систематизация знаний | 1 | Уроки 23-24. Обобщение и систематизация знаний. Контроль Ресурсы уроков. Учебник: «Подведём итоги», с. 132; Тетрадь-тренажёр: «Выполняем тест», с. 74; Поурочное тематическое планирование: «Обзорная работа», с. 66; Тетрадь-экзаменатор: Проверочные работы № 1, № 2, с. 36-39; Задачник-тренажёр: Дополнительные вопросы, «Построения на клетчатой бумаге», с. 82, 83 | Распознавать треугольники, прямоугольники на чертежах и рисунках, определять вид треугольников. Изображать треугольники, прямоугольники с помощью инструментов и от руки. Находить периметр треугольников, прямоугольников. Вычислять площади квадратов и прямоугольников. Решать задачи на нахождение периметров и площадей квадратов и прямоугольников. Исследовать свойства треугольников, прямоугольников путём эксперимента, наблюдения, измерения, моделирования, в том числе, с использованием компьютерных программ. Формулировать утверждения о свойствах треугольников, прямоугольников, равных фигур. Обосновывать, объяснять на примерах, опровергать с помощью контрпримеров утверждения о свойствах треугольников, прямоугольников, равных фигур. Конструировать алгоритм воспроизведения рисунков, построенных из треугольников, прямоугольников, строить по алгоритму, осуществлять самоконтроль, проверяя соответствие полученного изображения заданному рисунку. Конструировать орнаменты и паркеты, в том числе, с использованием компьютерных программ | | |
| 24 | Контрольная работа № 2 по теме «Треугольники и четырехугольники » | 1 | | | ||
| Глава 8. Дроби (13 уроков) Б5 | ||||||
| 25 | Основное свойство дроби | 5 | Уроки 25-29. Основное свойство дроби (п. 30). Основное свойство дроби. Равные дроби. Приведение дроби к новому знаменателю. Сокращение дробей. Ресурсы уроков. Учебник: теория, с. 140, 141, упр. № 491-508; Тетрадь- тренажёр: № 179, 196-198, 207-210, исследование — № 206; Задачник-тренажёр: № 276-299 | Формулировать основное свойство дроби и записывать его с помощью букв. Моделировать в графической форме и с помощью координатной прямой отношение равенства дробей. Применять основное свойство дроби к преобразованию дробей. Находить ошибки при сокращении дробей или приведении их к новому знаменателю и объяснять их. Анализировать числовые последовательности, членами которых являются дроби, находить правила их конструирования. Анализировать числовые закономерности, связанные с обыкновенными дробями. Применять дроби и основное свойство дроби при выражении единиц измерения величин в более крупных единицах | | |
| 26 | | | ||||
| 27 | | | ||||
| 28 | | | ||||
| 29 | | | ||||
| 30 | Сравнение обыкновенных дробей | 4 | Уроки 30-33. Сравнение дробей (п. 31)Сравнение дробей с одинаковыми знаменателями. Приведение дробей к общему знаменателю, сравнение дробей с разными знаменателями. Некоторые другие приемы сравнения дробей. Ресурсы уроков. Учебник: теория, с. 144-147, упр. № 509-525; Тетрадь- тренажёр: № 199, 200, 211, 212, исследование - № 206; Задачник-тренажёр: № 300-327 | Моделировать с помощью коордитнатной прямой отношения «больше» и «меньше» для обыкновенных дробей. Сравнивать дроби с равными знаменателями. Применять различные приёмы сравнения дробей с разными знаменателями, выбирая наиболее подходящий приём в зависимости от конкретной ситуации. Находить способы решения задач, связанных с упорядочиванием и сравнением дробей | | |
| 31 | | | ||||
| 32 | | | ||||
| 33 | | | ||||
| 34 | Обыкновенные дроби. Представление натуральных чисел дробями | 2 | Уроки 34-35. Натуральные числа и дроби (п. 32)Деление и дроби. Представление натуральных чисел дробями. Ресурсы уроков. Учебник: теория, с. 150, 151, упр. № 526-543; Тетрадь- тренажёр: № 201-203, 211, 212, исследование № 206 | Моделировать в графической и предметной форме существование частного для любых двух натуральных чисел. Оперировать символьными формами: записывать результат деления натуральных чисел в виде дроби, представлять натуральные числа обыкновенными дробями. Решать текстовые задачи, связанные с делением натуральных чисел, в том числе, задачи из реальной практики | | |
| 35 | | | ||||
| 36 | Обобщение и систематизация знаний | 2 | Уроки 105-106. Обобщение и систематизация знаний. Контроль Ресурсы уроков. Учебник: «Подведём итоги», с. 154; Тетрадь-тренажёр: «Выполняем тест», с. 89; Тетрадь-экзаменатор: Проверочные работы № 1,2 с. 40-45; Задачник-тренажёр: Дополнительные вопросы, «Находим НОД и НОК», с. 84 | Моделировать в графической, предметной форме понятия и свойства, связанные с понятием обыкновенной дроби (в том числе с помощью компьютера). Записывать и читать обыкновенные дроби. Соотноситьдроби и точки на координатной прямой. Преобразовывать дроби, сравнивать и упорядочивать их. Проводить несложные исследования, связанные со свойствами дробных чисел, опираясь на числовые эксперименты | | |
| 37 | Контрольная работа № 3 по теме «Дроби». | | | |||
| Глава 9. Действия с дробями (34 уроков)Б5 | ||||||
| 38 | Арифметические действия с дробями. Решение текстовых задач арифметическим способом | 6 | Уроки 38-43. Сложение и вычитание дробей (п. 33) Сложение и вычитание дробей с одинаковыми знаменателями. Сложение и вычитание дробей с разными знаменателями. Ресурсы уроков. Учебник: теория, с. 156, 157, упр. № 544-558; Задач- ник-тренажёр: № 328, 329, 338, 339, 341, 342, 330-337, 340, 434-346, 343; исследование — № 347, 348; Тетрадь- тренажёр: № 213, 216, 217, 219, 218. | Моделировать сложение и вычитание дробей с помощью реальных объектов, рисунков, схем. Формулировать и записывать с помощью букв правила сложения и вычитания дробей с одинаковыми знаменателями. Выполнять сложение и вычитание дробей с одинаковыми и с разными знаменателями, используя навыки преобразования дробей; дополнять дробь до 1. Применять свойства сложения для рационализации вычислений. Решать текстовые задачи, содержащие дробные данные | | |
| 39 | | | ||||
| 40 | | | ||||
| 41 | | | ||||
| 42 | | | ||||
| 43 | | | ||||
| 44 | Арифметические действия с дробями. Решение текстовых задач арифметическим способом | 6 | Уроки 44-49. Сложение и вычитание смешанных дробей (п. 34). Смешанная дробь. Выделение целой части из неправильной дроби и представление смешанной дроби в виде неправильной. Сложение и вычитание смешанных дробей. Ресурсы уроков. Учебник: теория, с. 160, 161, упр. № 559-577,579-587,590; исследование - №578,588, 589; Задачник-тренажёр:№ 349 -379, 381-382; исследование № 380; Тетрадь-тренажёр: № 220-223, исследование — № 225, 226 | Объяснять приём выделения целой части из неправильной дроби, представления смешанной дроби в виде неправильной и выполнять соответствующие записи. Выполнять сложение и вычитание смешанных дробей. Комментировать ход вычисления. Использовать приёмы проверки результата вычисления. Исследовать числовые закономерности | | |
| 45 | | | ||||
| 46 | | | ||||
| 47 | | | ||||
| 48 | | | ||||
| 49 | | | ||||
| 50 | Арифметические действия с дробями. Решение текстовых задач арифметическим способом | 5 | Уроки 50-54. Умножение дробей (п. 35). Правило умножения дробей. Умножение дроби на натуральное число и смешанную дробь. Решение задач. Ресурсы уроков. Учебник: теория, с.166,167, упр. № 592-610, исследование — № 611; Задачник-тренажёр: № 382-396, 399-405; исследование — № 397, 398; Тетрадь-тренажёр: исследование — № 227 | Формулировать и записывать с помощью букв правило умножения дробей. Выполнять умножение дробей, умножение дроби на натуральное число и на смешанную дробь. Вычислять значения числовых выражений, содержащих дроби; применять свойства умножения для рационализации вычислений. Проводить несложные исследования, связанные со свойствами дробных чисел, опираясь на числовые эксперименты (в том числе с помощью компьютера). Решать текстовые задачи, содержащие дробные данные ... | | |
| 51 | | | ||||
| 52 | | | ||||
| 53 | | | ||||
| 54 | | | ||||
| 55 | Арифметические действия с дробями. Решение текстовых задач арифметическим способом | 6 | Уроки 55-60. Деление дробей (п. 36) Взаимно обратные дроби. Правило деления дробей. Решение задач. Ресурсы уроков. Учебник: теория, с. 170, 171, упр. № 612-633, 635-646, исследование — № 634; Задачник-тренажёр:№ 406-436; Тетрадь-тренажёр: № 215, 224. исследование № 228 | Формулировать и записывать с помощью букв свойство взаимно обратных дробей, правило деления дробей. Выполнять деление дробей, деление дроби на натуральное число и наоборот, деление дроби на смешанную дробь и наоборот. Использовать приёмы проверки результата вычисления. Выполнять разные действия с дробями при вычислении значения выражения, содержащего несколько действий. Решать текстовые задачи, содержащие дробные данные, интерпретировать ответ задачи в соответствии с поставленным вопросом | | |
| 56 | | | ||||
| 57 | | | ||||
| 58 | | | ||||
| 59 | | | ||||
| 60 | | | ||||
| 61 | Нахождение части целого и целого по его части | 5 | Уроки 61-65. Нахождение части целого и целого по его части (п. 37) Нахождение части целого. Нахождение целого по его части. Ресурсы уроков. Учебник: теория, с. 176, 177, упр. № 647-656; Задачник-тренажёр: № 437-447 | Моделировать условие текстовой задачи с помощью рисунка; строить логическую цепочку рассуждений. Устанавливать соответствие между математическим выражением и его текстовым описанием. Решать задачи на нахождение части целого и целого по его части, опираясь на смысл понятия дроби, либо используя общий приём (умножение или деление на соответствующую дробь) | | |
| 62 | | | ||||
| 63 | | | ||||
| 64 | | | ||||
| 65 | | | ||||
| 66 | Решение текстовых задач арифметическим способом | 4 | Уроки 66-69. Задачи на совместную работу (п. 38)Решаем знакомую задачу. Задача на движение. Ресурсы уроков. Учебник: теория, с. 180, 181, упр. № 657-672 | Решать задачи на совместную работу. Использовать приём решения задач на совместную работу для решения задач на движение | | |
| 67 | | | ||||
| 68 | | | ||||
| 69 | | | ||||
| 70 | Обобщение и систематизация знаний. | 2 | Уроки 70-71. Обобщение и систематизация знаний. Контроль Ресурсы уроков. Учебник: «Подведём итоги», с. 184; Тетрадь-тренажёр: «Выполняем тест», с. 99, 100; Тетрадь-экзаменатор: Проверочные работы № 1, № 2 с. 46-57; Задачник-тренажёр: Дополнительные вопросы, «Старинные задачи на дроби», с. 85, 86 | Вычислять значения числовых выражений, содержащих дроби. Применять свойства арифметических действий для рационализации вычислений. Решать текстовые задачи, содержащие дробные данные. Использовать приёмы решения задач на нахождение части целого и целого по его части | | |
| 71 | Контрольная работа №4 по теме «Действия с дробями» | | | |||
| Глава 11. Таблицы и диаграммы (9 уроков)Б5 | ||||||
| 72 | Представление данных в виде таблиц | 3 | Уроки 72-74. Чтение и составление таблиц (п. 43) Как устроены таблицы. Чтение таблиц. Как составлять таблицы. Ресурсы уроков. Учебник: теория, с. 204, 205, упр. № 723-728; Тетрадь- тренажёр: № 263, 264, 266, 269, 271, 277, исследование — № 272; Задачник-тренажёр: № 448-453 | Знакомиться с различными видами таблиц. Анализировать готовые таблицы; сравнивать между собой представленные в таблицах данные из реальной практики. Заполнять простые таблицы, следуя инструкции | | |
| 73 | | | ||||
| 74 | | | ||||
| 75 | Представление данных в виде диаграмм | 2 | Уроки 75-76. Диаграммы (п. 44). Столбчатые диаграммы, чтение и построение диаграмм. Круговые диаграммы, чтение круговых диаграмм. Ресурсы уроков. Учебник: теория, с. 208, 209, упр. № 729-734; Тетрадь- тренажёр: № 265, 267-269, Задачник-тренажёр: № 454-462 | Знакомиться с такими видами диаграмм, как столбчатые и круговые диаграммы. Анализировать готовые диаграммы; сравнивать между собой представленные на диаграммах данные, характеризующие некоторое реальное явление или процесс. Строить в несложных случаях простые столбчатые диаграммы, следуя образцу | | |
| 76 | | | ||||
| 77 | Представление данных в виде таблиц и диаграмм | 2 | Уроки 77-78. Опрос общественного мнения (п. 45) Примеры опросов общественного мнения. Сбор и представление информации. Ресурсы уроков. Учебник: теория, с. 212,213,упр.№ 735-739; Тетрадь- тренажёр: № 270, 280, исследование № 273, 274; Задачник-тренажёр: № 463-466 | Знакомиться с примерами опроса общественного мнения и простейшими способами представления данных. Проводить несложные исследования общественного мнения, связанные с жизнью школы, внешкольными занятиями и увлечениями одноклассников: формулировать вопросы, выполнять сбор информации, представлять её в виде таблицы и столбчатой диаграммы | | |
| 78 | | | ||||
| 79 | Обобщение и систематизация знаний. | 2 | Уроки 160-161. Обобщение и систематизация знаний. Контроль. Учебник: «Подведём итоги», с. 216;. Тетрадь -экзаменатор: Проверочные работы № 1, № 2, с. 62-65 | Анализировать данные опросов общественного мнения, представленные в таблицах и на диаграммах, строить столбчатые диаграммы | | |
| 80 | Контрольная работа № 5 по теме «Таблицы и диаграммы». | | | |||
| Глава 2. Прямые на плоскости и в пространстве (7 уроков)Б6 | ||||||
| 81 | Взаимное расположение двух прямых. Пересекающиеся прямые. Перпендикулярные прямые. Вертикальные углы | 2 | Уроки 81-82. Пересекающиеся прямые (п. 6). Вертикальные углы. Перпендикулярные прямые. Смежные углы. Ресурсы уроков. Учебник: теория, с. 30, 31, упр. № 76-84, исследование № 85; Тетрадь-тренажёр: № 44 -46,51-53; исследование № 63 | Распознавать случаи взаимного расположения двух прямых. Распознавать вертикальные и смежные углы. Находить углы, образованные двумя пересекающимися прямыми. Изображать две пересекающиеся прямые, строить прямую, перпендикулярную данной. Выдвигать гипотезы о свойствах смежных углов, обосновывать их | | |
| 82 | | | ||||
| 83 | Взаимное расположение двух прямых. Параллельные прямые | 2 | Уроки 83-84. Параллельные прямые (п. 7). Параллельность. Снова перпендикулярность. Прямые в пространстве. Ресурсы уроков. Учебник: теория, с. 34, 35, упр. № 86-89, № 91-98, исследование — № 90; Тетрадь-тренажёр: № 47-49, 54-57, 62 | Распознавать случаи взаимного расположения двух прямых на плоскости и в пространстве, распознавать в многоугольниках параллельные стороны. Изображать две параллельные прямые, строить прямую, параллельную данной, с помощью чертёжных инструментов. Анализировать способ построения параллельных прямых, пошагово заданный рисунками, выполнять построения. Формулировать утверждения о взаимном расположении двух прямых, свойствах параллельных прямых | | |
| 84 | | | ||||
| 85 | Расстояние от точки до прямой, расстояние между параллельными прямыми | 2 | Уроки 85-86. Расстояние (п. 8) Расстояние между двумя точками. Расстояние от точки до фигуры. Расстояние между параллельными прямыми. Расстояние от точки до плоскости. Ресурсы уроков. Учебник: теория, с. 38, 39, упр. № 99-111; Тетрадь- тренажер: № 50, 58-60, 64, 65, исследование — № 61 | Измерять расстояние между двумя точками, от точки до прямой, между двумя параллельными прямыми, Строить геометрическое место точек, обладающих определенным свойством | | |
| 86 | | | ||||
| 87 | Обобщение и систематизация знаний | 1 | Урок 87. Обобщение и систематизация знаний. Контроль Ресурсы урока. Учебник: «Подведём итоги», с. 42; Тетрадь-тренажёр:«Выполняем тест», с. 32; Тетрадь-экзаменатор: Проверочные работы №, №2, с.12-15; Задачник: Доп. вопросы, «Задача о пауке и мухе», с. 90-92 от точки до плоскости. Строить параллельные прямые с заданным расстоянием между ними. | Распознавать случаи взаимного расположения положения двух прямых, распознавать в многоугольниках параллельные и перпендикулярные стороны. Изображать две пересекающиеся прямые, строить прямую, перпендикулярную данной, параллельную данной. Измерять расстояние между двумя точками, от точки до прямой, между двумя параллельными прямыми. Изображать многоугольники с параллельными, перпендикулярными сторонами | | |
| Глава 6. Отношения и проценты (17 уроков) | ||||||
| 88 | Отношение. Решение текстовых задач арифметическим способом | 2 | Уроки 88-89. Что такое отношение (п. 21) Отношение двух чисел. Деление в данном отношении. Решение задач на деление в данном отношении. Ресурсы уроков. Учебник: теория, с. 104, 105, упр. № 322-339; Тетрадь- тренажёр: № 144-147; 152, 153; Задачник: № 378-393 | Объяснять, что показывает отношение двух чисел, использовать и понимать стандартные обороты речи со словом «отношение». Составлять отношения, объяснять содержательный смысл составленного отношения. Решать задачи на деление чисел и величин в данном отношении, в том числе задачи практического характера | | |
| 89 | | | ||||
| 90 | Отношение. Решение текстовых задач арифметическим способом | 2 | Уроки 90-91. Отношение величин. Масштаб (п. 22) Отношение величин. Масштаб. Решение задач. Ресурсы уроков. Учебник: теория, с. 108, 109; упр. № 340-354; Тетрадь- тренажёр: № 148, 149, 154; Задачник: № 394-397; 400-403; исследование — № 398, 399 | Объяснять, как находят отношение одноимённых и разноимённых величин, находить отношения величин. Исследовать взаимосвязь отношений сторон квадратов, их периметров и площадей; длин рёбер кубов, площадей граней и объёмов. Объяснять, что показывает масштаб (карты, плана, чертежа, модели). Решать задачи практического характера на масштаб. Строить фигуры в заданном масштабе | | |
| 91 | | | ||||
| 92 | Проценты | 3 | Уроки 92-94. Проценты и десятичные дроби (п. 23) Представление процента десятичной дробью. Выражение дроби в процентах. Ресурсы уроков. Учебник: теория, с. 112, 113; упр. 355-369; Тетрадь- тренажёр: № 150, 151, 155-157, 162 | Выражать проценты десятичной дробью, выполнять обратную операцию — переходить от десятичной дроби к процентам. Характеризовать доли величины, используя эквивалентные представления заданной доли с помощью дроби и процентов | | |
| 93 | | | ||||
| 94 | | | ||||
| 95 | Нахождение процентов от величины и величины по её процентам. Решение текстовых задач арифметическим способом | 4 | Уроки 95-98. «Главная» задача на проценты (п. 24) Вычисление процентов от величины. Нахождение величины по ее проценту. Увеличение и уменьшение величины на несколько процентов. Округление и прикидка. Ресурсы уроков. Учебник: теория, с. 116, 117, упр. № 370-384; Тетрадь- тренажёр: № 158, 161; Задачник: № 404-424 | Решать задачи практического содержания на нахождение нескольких процентов величины, на увеличение (уменьшение) величины на несколько процентов, на нахождение величины по её проценту. Решать задачи с реальными данными на вычисление процентов величины, применяя округление, приёмы прикидки. Выполнять самоконтроль при нахождении процентов величины, используя прикидку | | |
| 96 | | | ||||
| 97 | | | ||||
| 98 | | | ||||
| 99 | Выражение отношения в процентах. Решение текстовых задач арифметическим способом | 4 | Уроки 99-102. Выражение отношения в процентах (п. 25) Нахождение процентного отношения. Решение текстовых задач. Округление и прикидка. Ресурсы уроков. Учебник: теория, с. 120, 121; упр. № 385-399; Тетрадь- тренажёр: № 159, 160; Задачник: № 425-440. | Выражать отношение двух величин в процентах. Решать задачи, в том числе задачи с практическим контекстом, с реальными данными, на нахождение процентного отношения двух величин. Анализировать текст задачи, моделировать условие с помощью схем и рисунков, объяснять полученный результат | | |
| 100 | | | ||||
| 101 | | | ||||
| 102 | | | ||||
| 103 | Обобщение и систематизация знаний. | 2 | Уроки 103-104. Обобщение и систематизация знаний. Контроль.Ресурсы уроков: Учебник: «Подведём итоги», с. 124; Тетрадь-тренажёр: «Выполняем тест», с. 76; Тетрадь -экзаменатор: Проверочные работы № 1, № 2, с. 32-37 | Находить отношения чисел и величин. Решать задачи, связанные с отношением величин, в том числе задачи практического характера. Решать задачи на проценты, в том числе задачи с реальными данными, применяя округление, приёмы прикидки | | |
| 104 | Контрольная работа №6 по теме «Отношения и проценты» | | | |||
| Глава 8. Симметрия (8 уроков) | ||||||
| 105 | Осевая и зеркальная сим метрии. Изображение симметричных фигур | 2 | Урок и 106-107. Осевая симметрия (п. 31). Точка, симметричная относительно прямой. Симметрия и равенство. Зеркальная симметрия. Ресурсы уроков. Учебник: теория, с. 148, 149, упр. № 473-484; Тетрадь- тренажёр: № 185, 188, 189, 191, 193, 194, 196
| Распознавать плоские фигуры, симметричные относительно прямой. Вырезать две фигуры, симметричные относительно прямой, из бумаги. Строить фигуру (отрезок, ломаную, треугольник, прямоугольник, окружность), симметричную данной относительно прямой, с помощью инструментов, изображать от руки. Проводить прямую, относительно которой две фигуры симметричны. Конструировать орнаменты и паркеты, используя свойство симметрии, в том числе с помощью компьютерных программ. Формулировать свойства двух фигур, симметричных относительно прямой. Исследовать свойства фигур, симметричных относительно плоскости, используя эксперимент, наблюдение, моделирование. Описывать их свойства формулам. Составлять уравнения условиям задач. Решать простейшие уравнения на основе зависимостей между компонентами арифметических дейст | | |
| 106 | | | ||||
| 107 | Осевая и зеркальная симметрии. Изображение симметричных фигур | 2 | Уроки 108-109. Ось симметрии фигуры (п. 32) Симметричная фигура. Прямоугольник, равнобедренный треугольник, окружность. Симметрия в пространстве. Ресурсы уроков. Учебник: теория, с. 152, 153, упр. № 485-498; Тетрадь- тренажёр: № 184, 190, 198, 203(а) | Находить в окружающем мире плоские и пространственные симметричные фигуры. Распознавать фигуры, имеющие ось симметрии. Вырезать их из бумаги, изображать от руки и с помощью инструментов. Проводить ось симметрии фигуры. Формулировать свойства равнобедренного, равностороннего треугольников, прямоугольника, квадрата, круга, связанные с осевой симметрией. Формулировать свойства параллелепипеда, куба, конуса, цилиндра, шара, связанные с симметрией относительно плоскости. Конструировать орнаменты и паркеты, используя свойство симметрии, в том числе с помощью компьютерных программ | | |
| 108 | | | ||||
| 109 | Центральная симметрия. Изображение симметричных фигур | 2 | Уроки 110-111. Центральная симметрия (п. 33) Симметрия относительно точки. Центр симметрии фигуры. Ресурсы уроков. Учебник: теория, с.156, 157,упр.№ 499 -512; Тетрадь-тренажёр:№ 187,192,195,197,199,200, 202, 203(6); исследование № 186,201 | Распознавать плоские фигуры, симметричные относительно точки. Строить фигуру, симметричную данной относительно точки, с помощью инструментов, достраивать, изображать от руки. Находить центр симметрии фигуры, конфигурации. Конструировать орнаменты и паркеты, используя свойство симметрии, в том числе с помощью компьютерных программ. Формулировать свойства фигур, симметричных относительно точки. Исследовать свойства фигур, имеющих ось и центр симметрии, используя эксперимент, наблюдение, измерение, моделирование, в том числе компьютерное моделирование. Выдвигать гипотезы, формулировать, обосновывать, опровергать с помощью контрпримеров утверждения об осевой и центральной симметрии фигур | | |
| 110 | | | ||||
| 111 | Обобщение и систематизация знаний. | 2 | Уроки 111-112. Обобщение и систематизация знаний. Контроль Ресурсы уроков. Учебник: «Подведём итоги», с. 160; Тетрадь-тренажёр: «Выполняем тест», с. 94; Тетрадь-экзаменатор: Проверочные работы № 1, № 2, с. 44-47; Задачник: Дополнительные вопросы, «Путешествие в Зазеркалье», с. 95-97 | Находить в окружающем мире плоские и пространственные симметричные фигуры. Распознавать плоские фигуры, симметричные относительно прямой, относительно точки, пространственные фигуры, симметричные относительно плоскости. Строить фигуру, симметричную данной относительно прямой, относительно точки с помощью чертёжных инструментов. Конструировать орнаменты и паркеты, используя свойство симметрии, в том числе с помощью компьютерных программ. Исследовать свойства фигур, имеющих ось и центр симметрии, используя эксперимент, наблюдение, измерение, моделирование, в том числе компьютерное моделирование. Формулировать, обосновывать, опровергать с помощью контрпримеров утверждения о симметрии фигур | | |
| 112 | Контрольная работа № 7 по теме «Симметрия». | | | |||
| Глава 9. Целые числа (13 уроков) | ||||||
| 113 | Положительные и отрицательные числа. Множество целых чисел | 1 | Урок 113. Какие числа называют целыми (п. 34) Числа, противоположные натуральным. Множество целых чисел. Ресурсы урока. Учебник: теория с. 162, 163, упр. № 513-527; Тетрадь- тренажёр: № 204, 205, 207, 210 -214 | Приводить примеры использования в жизни положительных и отрицательных чисел (температура, выигрыш- проигрыш, выше-ниже уровня моря и пр). Описывать множество целых чисел. Объяснять, какие целые числа называют противоположными. Записывать число, противоположное данному, с помощью знака «минус». Упрощать записи типа -(+3), -(-3) | | |
| 114 | Сравнение целых чисел | 2 | Уроки 114-115. Сравнение целых чисел (п. 35) Ряд целых чисел. Изображение целых чисел точками на координатной прямой. Сравнение и упорядочивание целых чисел. Ресурсы уроков. Учебник: теория с. 166, 167, упр. № 528-544, исследование — № 545; Тетрадь-тренажёр: № 206, 219-230, 250, 251 | Сопоставлять свойства ряда натуральных чисел и ряда целых чисел. Сравнивать и упорядочивать целые числа. Изображать целые числа точками на координатной прямой. Использовать координатную прямую как наглядную опору при решении задач на сравнение целых чисел | | |
| 115 | | | ||||
| 116 | Арифметические действия целыми числами. Свойства арифметических действий | 2 | Уроки 116-117. Сложение целых чисел (п. 36). Сложение двух целых чисел одного знака, разных знаков. Сумма противоположных чисел. Вычисление суммы нескольких целых чисел. Вычисление числовых значений буквенных выражений. Ресурсы уроков. Учебник: теория с. 170, 171, упр. № 546-563; Тетрадь- тренажёр: № 215-218, 231-234; Задачник: № 509-518 | Объяснять на примерах как находить сумму двух целых чисел. Записывать с помощью букв свойство нуля при сложении, свойство суммы противоположных чисел. Упрощать запись суммы целых чисел, опуская, где это возможно, знак « + » и скобки. Переставлять слагаемые в сумме целых чисел. Вычислять суммы целых чисел, содержащие два и более слагаемых. Вычислять значения буквенных выражений | | |
| 117 | | | ||||
| 118 | Арифметические действия с целыми числами. Свойства арифметических действий | 3 | Уроки 118-120. Вычитание целых чисел (п. 37) Правило нахождения разности двух целых чисел. Вычисление значений выражений, содержащих только действия сложения и вычитания. Вычисление значений буквенных выражений. Ресурсы уроков. Учебник: теория с. 174, 175, упр. № 564-581; Тетрадь- тренажёр: № 236-239, исследование — № 252; Задачник: № 519-526, 527-537 | Формулировать правило нахождения разности целых чисел, записывать его на математическом языке. Вычислять разность двух целых чисел. Вычислять значения числовых выражений, составленных из целых чисел с помощью знаков « + » и «-»; осуществлять самоконтроль. Вычислять значения буквенных выражений при заданных целых значениях букв. Сопоставлять выполнимость действия вычитания в множествах натуральных чисел и целых чисел | | |
| 119 | | | ||||
| 120 | | | ||||
| 121 | Арифметические действия с целыми числами. Свойства арифметических действий | 3 | Уроки 121-123. Умножение и деление целых чисел (п. 38) Умножение целых чисел. Деление целых чисел. Разные действия с целыми числами. Вычисление значений буквенных выражений. Ресурсы уроков. Учебник: теория с. 178, 179, упр. № 180, 181; Тетрадь- тренажёр: № 208, 209, 240-243, 244-246, 247-249, 256, исследование — № 253-255; Задачник: № 538-551, 552-562 | Формулировать правила знаков при умножении и делении целых чисел, иллюстрировать их примерами. Записывать на математическом языкеравенства, выражающие свойства 0 и 1 при умножении, правило умножения на -1. Вычислять произведения и частные целых чисел. Вычислять значения числовых выражений, содержащих разные действия с целыми числами. Вычислять значения буквенных выражений при заданных целых значениях букв. Исследовать вопрос об изменении знака произведения целых чисел при изменении на противоположные знаков множителей. Опровергать с помощью контрпримеров неверные утверждения о знаках результатов действий с целыми числами | | |
| 122 | | | ||||
| 123 | | | ||||
| 124 | Обобщение и систематизация знаний. | 2 | Уроки 124-125. Обобщение и систематизация знаний. Контроль Ресурсы уроков. Учебник: «Подведём итоги», с. 182; Тетрадь-тренажёр: «Выполняем тест», с. 112; Тетрадь-экзаменатор: Проверочные работы № 1, № 2, с. 48-53; Задачник: Дополнительные вопросы, «В худшем случае», с. 97-99 | Сравнивать, упорядочивать целые числа. Формулировать правила вычисления с целыми числами, находить значения числовых и буквенных выражений, содержащих действия с целыми числами | | |
| 125 | Контрольная работа № 8 по теме «Целые числа.» | | | |||
| Глава 10. Рациональные числа (18 уроков) | ||||||
| 126 | Множество рациональных чисел. Изображение чисел точками координатной прямой | 3 | Уроки 126-128. Какие числа называют рациональными (п. 39) Рациональные числа: положительные и отрицательные числа (целые и дробные); противоположные числа. Изображение рациональных чисел точками координатной прямой. Ресурсы уроков. Учебник: теория, с. 184, 185, упр. № 599-614; Тетрадь- тренажёр: № 259-266 | Применять в речи терминологию, связанную с рациональными числами; распознавать натуральные, целые, дробные, положительные, отрицательные числа; характеризовать множество рациональных чисел. Применять символьное обозначение противоположного числа, объяснять смысл записей типа (-а), упрощать соответствующие записи. Изображать рациональные числа точками координатной прямой | | |
| 127 | | | ||||
| 128 | | | ||||
| 129 | Сравнение рациональных чисел | 2 | Уроки 129-130. Сравнение рациональных чисел. Модуль числа (п. 40). Сравнение рациональных чисел с помощью координатной прямой. Установление отношений «больше» («меньше») между рациональными числами. Понятие модуля числа. Ресурсы уроков: Учебник: теория, с. 188, 189, упр. № 615-629; Тетрадь- тренажёр: № 257, 258, 267-269, 284, 285; Задачник: № 563-580 | Моделировать с помощью координатной прямой отношения «больше» и «меньше» для рациональных чисел. Сравнивать положительное число и нуль, отрицательное число и нуль, положительное и отрицательное числа, два отрицательных числа. Применять и понимать геометрический смысл понятия модуля числа, находить модуль рационального числа. Сравнивать и упорядочивать рациональные числа | | |
| 130 | | | ||||
| 131 | Арифметические действия с рациональными числами. Свойства арифметических действий | 3 | Уроки 131-133. Сложение и вычитание рациональных чисел (п. 41). Правила сложения рациональных чисел одного знака, разных знаков. Свойства сложения, свойство нуля при сложении. Вычитание рациональных чисел. Ресурсы уроков. Учебник: теория, с. 192, 193, упр. № 630-645; исследование — № 646; Тетрадь-тренажёр: № 270-275; Задачник: № 581-593 | Формулировать правила сложения двух чисел одного знака, двух чисел разных знаков; правило вычитания из одного числа другого; применять эти правила для вычисления сумм, разностей. Выполнять числовые подстановки в суммы и разности, записанные с помощью букв, находить соответствующие их значения. Проводить несложные исследования, связанные со свойствами суммы нескольких рациональных чисел (например, замена знака каждого слагаемого) | | |
| 132 | | | ||||
| 133 | | | ||||
| 134 | Арифметические действия с рациональными числами. Свойства арифметических действий | 3 | Уроки 134-136. Умножение и деление рациональных чисел (п. 42) Умножение и деление рациональных чисел, правила знаков при умножении и делении. Свойства умножения, свойства 0, 1 и -1 при умножении. Равество Ресурсы уроков. Учебник: теория, с. 196, 197, упр. № 647-669; Тетрадь-тренажёр: № 276, 277; Задачник: № 594-627 | Формулировать правила нахождения произведения и частного двух чисел одного знака, двух чисел разных знаков; применять эти правила при умножении и делении рациональных чисел. Находить квадраты и кубы рациональных чисел. Вычислять значения числовых выражений, содержащих разные действия. Выполнять числовые подстановки в простейшие буквенные выражения, находить соответствующие их значения | | |
| 135 | | | ||||
| 136 | | | ||||
| 137 | Декартовы координаты на плоскости | 5 | Уроки 137 -141. Координаты (п. 43) Примеры различных систем координат в окружающем мире. Прямоугольная система координат на плоскости, координаты точки. Ресурсы уроков. Учебник: теория, с. 200, 201, упр. № 670-683; исследование — № 684; Тетрадь-тренажёр: № 278-283; 288, исследование — № 286, 287
| Приводить примеры различных систем координат в окружающем мире, находить и записывать координаты объектов в различных системах координат (шахматная доска; широта и долгота; азимут и др.). Объяснять и иллюстрировать понятие прямоугольной системы координат на плоскости; применять в речи и понимать соответствующие термины и символику. Строить на координатной плоскости точки и фигуры по заданным координатам, находить координаты точек. Проводить исследования, связанные с взаимным расположением точек на координатной плоскости | | |
| 138 | | | ||||
| 139 | | | ||||
| 140 | | | ||||
| 141 | | | ||||
| 142 | Обобщение и систематизация знаний. | | Уроки 142-143. Обобщение и систематизация знаний. Контроль Ресурсы уроков: Учебник: «Подведём итоги», с. 204; Тетрадь-тренажёр: «Выполняем тест», с. 128; Тетрадь-экзаменатор: Проверочные работы № 1, № 2, с. 54-59; Задачник: Дополнительные вопросы, «Системы счисления», с. 99-102
| Изображать рациональные числа точками координатной прямой. Применять и понимать геометрический смысл понятия модуля числа, находить модуль рационального числа. Моделировать с помощью координатной прямой отношения «больше и «меньше» для рациональных чисел, сравнивать и упорядочивать рациональные числа. Выполнять вычисления с рациональными числами.. Находить значения буквенных выражений при заданных значения букв. Строить на координатной плоскости точки и фигуры по заданным координатам, определять координаты точек | | |
| 143 | Контрольная работа № 9 по теме «Рациональные числа». | | | |||
| §8. Решение уравнений. ( 14 часов) | ||||||
| 144 | п 39 Раскрытие скобок | 3 | Уроки 144-146. Раскрытие скобок. Ресурсы урока. Учебник с.214-216, упр. №№ 1234,1235, 1239 – 1241,1245, 1237,1238,1242,1249- задача исследование.
| - Правильно использовать в речи термины: коэффициент, раскрытие скобок, подобные слагаемые, приведение подобных слагаемых, корень уравнения, линейное уравнение. - Грамматически верно читать записи уравнений. - Раскрывать скобки, упрощать выражения, вычислять коэффициент выражения. - Решать уравнения умножением или делением обеих его частей на одно и то же не равное нулю число, путем переноса слагаемого из одной части уравнения в другую. Решать текстовые задачи с помощью уравнений. - Решать текстовые задачи арифметическими способами. - Приводить примеры конечных и бесконечных множеств. - Решать логические задачи с помощью графов. | | |
| 145 | | | ||||
| 146 | | | ||||
| 147 | п 40 Коэффициент | 1 | Урок 147. Коэффициент. Ресурсы урока. Учебник с. 220,221, упр. №№1261, 1262, 1297,1271 |
| | |
| 148 | п 41 Подобные слагаемые | 3 | Урок 148-150. Подобные слагаемые. Ресурсы урока. Учебник с.224,225, упр. №№ 1281-1283, 1284,1287,задача исследование- 1292 | | | |
| 149 | | | ||||
| 150 | | | ||||
| 151 | Контрольная работа № 10 по теме "Раскрытие скобок" | 1 | Урок 151. Решение контрольной работы по вариантам | | | |
| 152 | Анализ контрольной работы. п 42 Уравнение, корень уравнения. | 1 | Урок 152-153. Уравнение, корень уравнения. Ресурсы урока. Учебник с.229,230, упр. №№ 1314-1317,1321,1316, 1317 | | | |
| 153 | п 42 Нахождение неизвестных компонентов арифметических действий. | 1 | | | ||
| 154 | п 42 Решение уравнений | 2 | Урок 154- 155. Решение уравнений. Ресурсы урока. Учебник с. 229,230, упр. №№ 1320, 1334,1324, 1320 | | | |
| 155 | | | ||||
| 156 | Контрольная работа № 11 по теме "Решение уравнений" | 1 | Урок 156. Решение контрольной работы по вариантам | | | |
| 157 | Анализ контрольной работы. Решение задач | 1 | Урок 157. Решение задач. |
| | |
| Глава 12. Множества. Комбинаторика (8 уроков) | ||||||
| 158 | Множество, элемент множества. Задание множеств перечислением элементов, характеристическим свойством. Стандартные обозначения числовых множеств. Пустое множество. Подмножества | 2 | Уроки 158-160. Понятие множества (п. 48) Множество, элемент множества. Задание множеств перечислением элементов, характеристическим свойством. Стандартные обозначения числовых множеств. Пустое множество и его обозначение. Подмножество, иллюстрация отношения включения с помощью кругов Эйлера. Ресурсы уроков. Учебник: теория с. 224, 225, упр. № 737-749, исследование — № 750; Тетрадь-тренажёр: № 318, 321, 322, 335, исследование — № 336; Задачник: № 628-636, исследование — № 637 | Обсуждать соотношение между основными числовыми множествами. Записывать на символическом языке соотношения между множествами и приводить примеры различных вариантов их перевода на русский язык. Исследовать вопрос о числе подмножеств конечного множества | | |
| 159 | | | ||||
| 160 | Объединение и пересечение множеств. Иллюстрация отношений между множествами с помощью диаграмм Эйлера-Венна | 2 | Уроки 160-161. Операции над множествами (п. 49) Объединение множеств, пересечение множеств; иллюстрации с помощью кругов Эйлера. Понятие о классификации. Ресурсы уроков. Учебник: теория с. 228, 229, упр. № 751-763; Тетрадь-тренажёр: № 319, 320, 323-326, исследование — № 334; Задачник: № 638-645, 646-653 | Формулировать определения объединения и пересечения множеств. Иллюстрировать эти понятия с помощью кругов Эйлера. Использовать схемы в качестве наглядной основы для разбиения множества на непересекающиеся подмножества. Проводить логические рассуждения по сюжетам текстовых задач с помощью кругов Эйлера. Приводить примеры классификаций из математики и из других областей знания | | |
| 161 | | | ||||
| 162 | Решение комбинаторных задач перебором вариантов | 4 | Уроки 162-165. Решение комбинаторных задач (п. 50) Решение комбинаторных задач перебором вариантов, построение дерева возможных вариантов.Теоретико-множественные модели некоторых комбинаторных задач. Ресурсы уроков. Учебник: теория с. 232, 233, упр. № 764-777; Тетрадь- тренажёр: № 327-333; Задачник: № 654-669 | Решать комбинаторные задачи с помощью перебора возможных вариантов, в том числе, путём построения дерева возможных вариантов. Строить теоретико-множественные модели некоторых видов комбинаторных задач | | |
| 163 | | | ||||
| 164 | | | ||||
| 165 | | | ||||
| Повторение.(10 ч.) | ||||||
| 166 | Повторение и итоговый контроль | 10 | Уроки 166-175. Повторение и итоговый контроль Ресурсы уроков. Тетрадь-экзаменатор: Итоговые работы за год № 1, № 2, с. 70-78 | Сравнивать и упорядочивать десятичные дроби, находить наименьшую и наибольшую десятичную дробь среди заданного набора чисел. Представлять обыкновенные дроби в виде десятичных; выяснять, в каких случаях это возможно. Находить десятичное приближение обыкновенной дроби с указанной точностью. Выполнять действия с дробными числами. Решать задачи на движение, содержащие данные, выраженные дробными числами. Представлять доли величины в процентах. Решать текстовые задачи на нахождение процента от данной величины. Решать задачи, требующие владения понятием отношения. Составлять по рисунку формулу для вычисления периметра или площади фигуры. Сравнивать и упорядочивать положительные и отрицательные числа, находить наибольшее или наименьшее из заданного набора чисел. Выполнять числовые подстановки в буквенное выражение (в том числе, подставлять отрицательные числа), вычислять значение выражения. Отмечать точки на координатной плоскости, находить координаты отмеченных точек. Строить фигуру, симметричную данной относительно некоторой прямой; использовать при решении задач равенство симметричных фигур. Решать задачи на взаимное расположение двух окружностей на плоскости | | |
| 167 | | | ||||
| 168 | | | ||||
| 169 | | | ||||
| 170 | | | ||||
| 171 | | | ||||
| 172 | | | ||||
| 173 | | | ||||
| 174 | | | ||||
| 175 | | | ||||
Дополнительная литература.
1. Бунимович Е.А. Математика. Арифметика. Геометрия. 5 класс: учебник для общеобразоват. учреждений./ Е.А. Бунимович, Г.В. Дорофеев, С.Б. Суворова и др. — М.: Просвещение, 2017.
2. Бунимович Е.А. Математика. Арифметика. Геометрия. Тетрадь-тренажёр. 5 класс: пособие для учащихся общеобразоват. учреждений. / Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева и др. — М. : Просвещение, 2010.
3. Бунимович Е.А.. Математика. Арифметика. Геометрия. Задачник-тренажёр. 5 класс: пособие для учащихся общеобразоват. учреждений. / Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева и др. — М. : Просвещение, 2010.
4.Сафонова Н.В. Математика. Арифметика. Геометрия. Тетрадь-экзаменатор. 5 класс: пособие для учащихся общеобразоват. учреждений. — М.: Просвещение, 2010.
5.Кузнецова Л.В. Математика. Поурочное тематическое планирование 5 класс: пособие для учителей общеобразоват. учреждений. / Л.В. Кузнецова, С.С. Минаева, Л.О. Рослова и др. — М.: Просвещение, 2010.
1.Бунимович Е.А. Математика. Арифметика. Геометрия. 6 класс: учебник для общеобразоват. учреждений. / Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева и др. — М.: Просвещение, 2010.
3. Бунимович Е.А. Математика. Арифметика. Геометрия. Тетрадь-тренажёр. 6 класс: пособие для учащихся общеобразоват. учреждений. / Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева и др. — М. : Просвещение, 2010.
4. Бунимович Е.А. Математика. Арифметика. Геометрия. Задачник. 6 класс: пособие для учащихся общеобразоват. учреждений. / Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева и Ф. — М. : Просвещение, 2010.
5. Кузнецова Л.В. Математика. Арифметика. Геометрия. Тетрадь - экзаменатор. 6 класс: пособие для учащихся общеобразоват. учреждений. / Л.В. Кузнецова, С.С. Минаева, Л.С. и др. М. : Просвещение, 2010.
6. Кузнецова Л.В. Математика. Поурочное тематическое планирование 6 класс: пособие для учителей общеобразоват. учреждений. / Л.В. Кузнецова, С.С. Минаева, Л.О. Рослова и др М. : Просвещение, 2011
Оснащение процесса обучения математике обеспечивается библиотечным фондом, печатными пособиями, а также информационно-коммуникативными средствами, экранно-звуковыми пособиями, техническими средствами обучения, учебно-практическим и учебно-лабораторным оборудованием.
Технические средства обучения:
мультимедийный компьютер;
мультимедиапроектор;
интерактивная доска.
Информационные средства:
коллекция медиаресурсов, электронные базы данных;
Интернет. Гиперссылки на ресурс:http://eorhelp.ru/
http://www.fcior.edu.ru
http://www.school-collection.edu.ru
http://www.openclass.ru/
http://powerpoint.net.ru/
http://karmanform.ucoz.ru/
Учебно-практическое и учебно-лабораторное оборудование:
доска магнитная с координатной сеткой;
комплект чертежных инструментов (классных и раздаточных): линейка, транспортир, угольник (30°, 60°), угольник (45°, 45°), циркуль;
комплекты планиметрических и стереометрических тел (демонстрационный и раздаточный);
комплекты для моделирования (цветная бумага, картон, калька, клей, ножницы, пластилин).
Печатные пособия:
таблицы по математике для 5 -6 классов;
портреты выдающихся деятелей математики.
- Сайт интернет-поддержки УМК «Сферы»: www.sрhегеs.ги
Контрольные работы.
Глава 6. Делимость чисел
Контрольная работа № 1.
Вариант 1
Запишите какие-нибудь четыре делителя числа 45.
Найдите все общие делители чисел 60 и 45.
Разложите на простые множители число 72.
Какие из чисел 618, 567, 7587, 91754 делятся на 2, 3, 9?
Делится ли сумма 1980 + 396 на 5? на 3?
Нужно упаковать 87 теннисных мячей по 4 штуки с одну коробку. Сколько таких коробок получится? Сколько мячей останется неупакованными?
*Запишите наибольшее четырёхзначное число, делящееся на 18.
В вагоне 36 мест по 4 места в каждом купе. Определите номер купе, в котором находится 18 место.
Глава 6. Делимость чисел
Контрольная работа № 1.
Вариант 2
Запишите какие-нибудь четыре числа, кратные 8.
Найдите все общие делители чисел 24 и 42.
Разложите на простые множители число 48.
Какие из чисел 444, 601, 1256, 8652 делятся на 2, 3, 9?
Делится ли произведение чисел 387• 2251 на 2? на 9?
Нужно упаковать 1500г конфет по 200 г в одну коробку. Сколько таких коробок получится? Сколько граммов конфет останется неупакованными?
*Запишите наименьшее пятизначное число, делящееся на 6.
*Фёдору нужно прочитать книгу. Он решил, что будет читать по 15 страниц в день. На какой день он будет на 83-й странице?
Глава 7 «Треугольники и четырёхугольники»
Контрольная работа № 2
1 вариант
Найдите площадь прямоугольника со сторонами 20 см и 16 см.
Какая из данных величин выражает площадь песочницы на детской площадке? а) 4 км²; б) 4м²; в) 4 дм²; г) 4 см²
Какой треугольник изображён на рисунке?


Определите площадь фигуры, если площадь одного квадрата равна 4 см²
На рисунке изображён квадрат. Для каждого утверждения определите, верное оно или неверное. а) треугольник ABC-прямоугольный и равнобедренный. б) диагональ делит квадрат на 2 равных треугольника. в) площадь треугольника ABD больше площади квадрата.
Начертите прямоугольный треугольник и обозначьте его. Найдите периметр треугольника. Запишите, является ли ваш треугольник равнобедренным, равносторонним.
Постройте прямоугольник со сторонами 4 см и 3 см. Обозначьте его. Вычислите периметр прямоугольника. Проведите диагонали и вычислите величину угла между диагоналями.
Глава 7 «Треугольники и четырёхугольники»
Контрольная работа № 2
2 вариант
Найдите площадь квадрата со стороной 15 мм.
Для каждой измеряемой площади подберите единицу измерения: комната; книга; сквер; город. (км²; м²; га; см²)
Какой треугольник изображён на рисунке?


Определите площадь фигуры, если площадь одного квадрата равна 4 см²
На рисунке изображён прямоугольник. Для каждого утверждения определите, верное оно или неверное. а) диагонали прямоугольника равны. б) треугольник ABC-прямоугольный и равнобедренный в) площадь прямоугольника равна произведению сторон BC и CD.
Начертите остроугольный треугольник и обозначьте его. Найдите периметр треугольника. Запишите, является ли ваш треугольник равнобедренным, равносторонним.
Постройте квадрат со стороной 4 см. Обозначьте его. Вычислите периметр квадрата. Проведите диагонали и вычислите величину угла между диагональю и стороной квадрата.
Глава 8. Дроби
Контрольная работа № 3. Вариант 1
Начертите прямоугольник со сторонами 6 клеток и 4 клетки. Закрасьте
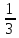 прямоугольника.
прямоугольника.Сколько минут а) в
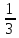 ч; б) в
ч; б) в 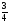 часа?
часа?Сократите дробь
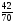 .
.Выпишите дроби, равные
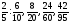 .
. Сравните числа
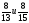
Приведите дроби
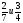 к общему знаменателю
к общему знаменателюСократите дробь
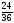
*Запишите какое-нибудь число, больше
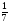 , но меньше
, но меньше 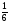 .
.*Укажите наибольшее из чисел
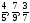 .
.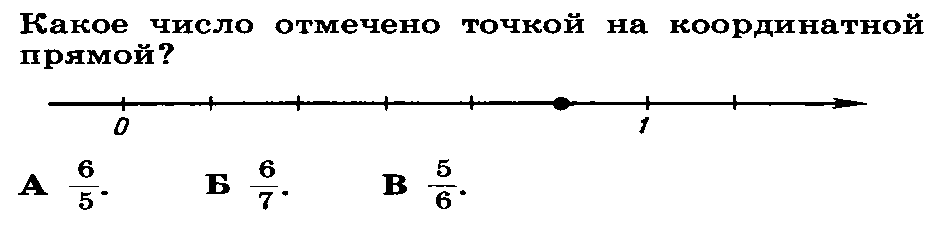
Глава 8. Дроби
Контрольная работа № 3. Вариант 2
Начертите квадрат со стороной 6 клеток. Закрасьте
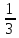
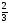 квадрата.
квадрата.Сколько часов а)
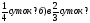
Сократите дробь
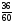 .
.Выпишите дроби, равные
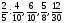 .
. Сравните числа
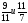
Приведите дроби
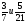 к общему знаменателю
к общему знаменателюСократите дробь
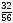
*Запишите какое-нибудь число, больше 1, но меньше
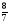
*Укажите наибольшее из чисел
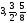 .
.


Глава 9. Действия с дробями
Контрольная работа № 4. Вариант 1
Представьте в виде неправильной дроби 2
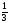 . Выделите целую часть
. Выделите целую часть 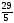 .
.Выполните действия: а)
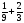 ; б)
; б) 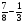 ; в) 2
; в) 2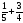 ; г)2-1
; г)2-1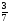
Выполните действия: а)
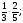 б)
б) 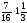 ; в) 10
; в) 10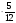 ; г)
; г) 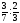 ; д)
; д) 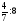 .
.В одном пакете 1
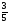 кг яблок, а в другом на
кг яблок, а в другом на 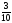 кг больше. Сколько килограммов яблок в двух пакетах
кг больше. Сколько килограммов яблок в двух пакетахВ олимпиаде участвовало 300 школьников,
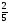 из них прошли в следующий тур. Сколько участников будут проходить испытания в следующем туре олимпиады?
из них прошли в следующий тур. Сколько участников будут проходить испытания в следующем туре олимпиады?Ира может вскопать грядку за 4 часа, а Митя – за 3 часа. За какое время они вскопают грядку, работая одновременно?
Найдите значение выражения 7-1
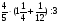
Глава 9. Действия с дробями
Контрольная работа № 4. Вариант 2
Представьте в виде неправильной дроби 4
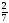 . Выделите целую часть
. Выделите целую часть 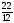 .
.Выполните действия: а)
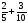 ; б)
; б) ; в) 4
; г) 3 -1
.
Выполните действия: а)
; б)2
; в) 6
; г)
; д) 7:2
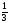 .
.От мотка проволоки длиной 6 м отрезали сначала 3
м, а затем ещё
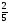 м. Сколько метров проволоки осталось в мотке?
м. Сколько метров проволоки осталось в мотке?В поход отправились 24 пятиклассника,
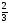 из них – мальчики. Сколько мальчиков пошло в поход?
из них – мальчики. Сколько мальчиков пошло в поход?Лена надула
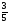 всех шаров, Денис -
всех шаров, Денис - 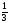 . А Семён – оставшиеся 6 шаров. Сколько шаров надул Денис?
. А Семён – оставшиеся 6 шаров. Сколько шаров надул Денис?Найдите значение выражения 5-8
Глава 11. Таблице и диаграммы
Контрольная работа № 5. Вариант 1
Среди пятиклассников провели опрос «Куда бы вы хотели пойти в выходной день?» При ответе можно было выбрать только один вариант ответа из предложенных. В опросе принимали участие все учащиеся 5А и 5Б классов. В таблице приведены результаты проведённого опроса.
| Вид досуга | Классы | Всего | |||||||
| 5А | 5Б | девочки | мальчики | ||||||
| девочки | мальчики | девочки | мальчики |
|
| ||||
| Кино | 1 | 5 | 2 | 2 |
|
| |||
| Театр | 3 | 2 | 4 | 1 |
|
| |||
| Экскурсия | 5 | 4 | 5 | 5 |
|
| |||
| Прогулка | 4 | 5 | 1 | 7 |
|
| |||
1.Заполните столбцы «Всего»
2.Сколько девочек 5Б класса хотят пойти на экскурсию?
3.Сколько мальчиков в 5А классе?
4.Какой вид досуга наиболее популярен среди мальчиков 5Б класса?
5.Какой вид досуга наименее популярен у девочек?
6Какой вид досуга наиболее популярен среди пятиклассников?
7.По результатам опроса постройте столбчатую диаграмму.
Глава 11. Таблице и диаграммы
Контрольная работа № 5. Вариант 2
Среди пятиклассников провели опрос «Куда бы вы хотели пойти в выходной день?» При ответе можно было выбрать только один вариант ответа из предложенных. В опросе принимали участие все учащиеся 5А и 5Б классов. В таблице приведены результаты проведённого опроса.
| Вид досуга | Классы | Всего | |||||||
| 5А | 5Б | девочки | мальчики | ||||||
| девочки | мальчики | девочки | мальчики |
|
| ||||
| Кино | - | 1 | 1 | 2 |
|
| |||
| Театр | 7 | 4 | 5 | 4 |
|
| |||
| Экскурсия | 4 | 8 | 5 | 5 |
|
| |||
| Прогулка | 2 | 3 | 1 | 4 |
|
| |||
1.Заполните столбцы «Всего»
2. Какой вид досуга наиболее популярен у девочек?
3.Сколько мальчиков 5А класса предпочитают экскурсию?
4.Сколько мальчиков в 5Б классе?
5.Сколько девочек в двух классах?
6Какой вид досуга наиболее популярен среди пятиклассников?
7.По результатам опроса постройте столбчатую диаграмму.
Контрольная работа №6: «Отношения и проценты»
Вариант 1
Отрезок
разделен точкой
на две части так, что . Найдите отношение
к
.
Школьная футбольная команда за год провела 20 матчей, не сыграв ни одного вничью. Число выигранных матчей относится к числу проигранных как
. Сколько матчей команда выиграла?
Масштаб карты 1
. Во сколько раз расстояние между двумя пунктами на местности больше расстояния между соответствующими точками на карте? Чему равно расстояние между пунктами
и
в действительности, если на карте оно равно 3 см?
В начале года в школе было 600 учащихся. За год число учащихся уменьшилось на 9%. Сколько учащихся осталось в школе к концу учебного года?
Для выращивания рассады гороха посадили 60 семян, из которых проросло 48. Сколько процентов семян проросло?
Железнодорожный билет от города до города
стоил 400 р. Его стоимость была повышена на 20%, а через год еще на 10% от его предыдущей цены. Сколько стал стоить билет?
Отношение длин сторон прямоугольника равно
. Найдите площадь этого прямоугольника, если длина меньшей стороны равна 12 см.
Вариант 2
Отрезок
разделен точкой
на две части так, что . Найдите отношение
к
.
Школьная команда шахматистов за год участвовала в 16 турнирах, занимая каждый раз только первые или вторые места, которые распределились в отношении
. Сколько раз команда завоевала первое место?
Масштаб карты 1
. Во сколько раз расстояние между двумя пунктами
и
на местности больше соответствующего расстояния на карте? Чему равно расстояние между пунктами
и
в действительности, если на карте оно равно 14 см?
В начале года в школе было 500 учащихся. За год число учащихся увеличилось на 8%. Сколько учащихся обучалось в школе к концу учебного года?
Для выращивания рассады фасоли посадили 50 семян, из которых проросло 45. Сколько процентов семян проросло?
В августе на базу приехали 400 человек, в сентябре число отдыхающих уменьшилось на 20%, а в октябре на 30% по сравнению с сентябрем. Сколько отдыхающих было на базе в октябре?
Отношение длин сторон прямоугольника равно
. Найдите площадь этого прямоугольника, если длина большей стороны равна 20 см.
Контрольная работа № 7 «Симметрия»
Вариант 1.
Постройте прямую с и точку В, не лежащую на прямой с. Постройте для точки В симметричную точку относительно прямой с.
Постройте отрезок АВ и точку О, не лежащую на отрезке АВ. Постройте для отрезка АВ симметричный отрезок относительно точки О.
Постройте произвольный треугольник АВС и прямую k, не пересекающую треугольник АВС. Постройте треугольник симметричный данному относительно прямой k.
Постройте четырехугольник АВСД и точку F, вне этого четырехугольника. Постройте фигуру симметричную данной относительно точки F.
Постройте произвольный пятиугольник и точку О внутри него. Постройте фигуру симметричную данной относительно точки О.
Постройте фигуру, имеющую одну ось симметрии; бесконечное множество осей симметрии.
Контрольная работа № 7 «Симметрия»
Вариант 2.
Постройте точки А и О. Постройте для точки А симметричную точку относительно точки О.
Постройте отрезок ВС и прямую n, не пересекающую отрезок ВС. Относительно прямой n, постройте отрезок симметричный отрезку ВС.
Постройте произвольный треугольник АВС и точку R вне этого треугольника. Постройте фигуру симметричную данному треугольнику относительно точки R.
Постройте произвольный четырехугольник АВСД и прямую а, пересекающую стороны ВС и АД. Постройте фигуру симметричную данной относительно прямой а.
Постройте произвольный пятиугольник и точку М, вне этого пятиугольника. Постройте фигуру симметричную данной относительно точки М.
Постройте центрально симметричную фигуру; постройте фигуру не имеющую центра симметрии.
Контрольная работа №8: «Целые числа»
Вариант 1
Сравните числа: а)
и
; б)
и
.
Запишите в порядке убывания числа
Вычислите: а)
; б)
; в)
; г)
; д)
; е)
; ж)
; з)
Найдите значение выражения: а)
; б)
.
Дано равенство
. Найдите число
.
Найдите значение выражения
при
.
Вариант 2
Сравните числа: а)
и
; б)
и
.
Запишите в порядке возрастания числа
Вычислите: а)
; б)
; в)
; г)
; д)
; е)
; ж)
; з)
Найдите значение выражения: а)
; б)
.
Дано равенство
. Найдите число
.
Найдите значение выражения
при
.
Контрольная работа №9: «Рациональные числа»
Вариант 1
Для каждого числа
запишите противоположное ему число
.
а) ; б)
.
Начертите координатную прямую, взяв за единичный отрезок 20 клеток и отметьте на ней все числа с одним знаком после запятой, которые расположены между
и
.
Замените выражение равным ему числом: а)
; б)
.
Найдите модуль числа и запишите ответ с помощью знака модуля. а)
; б)
.
Сравните числа: а)
и
; б)
и
.
Вычислите: а)
; б)
; в)
г)
; д)
.
Выпишите все целые числа, модуль которых больше 1, но меньше 3.
Найдите значение выражения
На координатной плоскости постройте треугольник
, координаты вершин которого равны
,
,
. Постройте треугольник, симметричный треугольнику
относительно оси
, обозначьте его вершины и запишите их координаты.
Вариант 2
Для каждого числа
запишите противоположное ему число
.
а) ; б)
.
Начертите координатную прямую, взяв за единичный отрезок 20 клеток и отметьте на ней все числа с одним знаком после запятой, которые расположены между
и
.
Замените выражение равным ему числом: а)
; б)
.
Найдите модуль числа и запишите ответ с помощью знака модуля. а)
; б)
.
Сравните числа: а)
и
; б)
и
.
Вычислите: а)
; б)
; в)
г)
; д)
Выпишите все целые числа, модуль которых меньше 5, но больше 2.
Найдите значение выражения
На координатной плоскости постройте треугольник
, координаты вершин которого равны
,
,
. Постройте треугольник, симметричный треугольнику
относительно оси
, обозначьте его вершины и запишите их координаты.
Контрольная работа №10 по теме: «Раскрытие скобок. Подобные слагаемые».
Вариант 1
№1 Найдите значение выражения:
А) 23,6 + (14,5 – 30,1) – (6,8 + 1,9)
Б) 20,9 – (14,8 + 17,9) – (6,6 – 15,7)
№2 Упростите выражение и найдите значение:
А) x – 0,2y – 0,7 x +10 + 0,5y – 0,3 - 18
при х =100,1 и у = - 30
Б) -8n – (4n – 6k), если k - 2n=11
№3 Решите уравнение:
А) 0,7х - 0,4х - 0,97х = 12,73
Б) 0,3(х – 2) – 0,2(х + 4) = 0,6
№4 Решите задачу:
Турист проехал на поезде и теплоходе 605 км. Средняя скорость поезда 60км/ч, средняя скорость теплохода 25 км/ч. Сколько времени турист ехал на поезде и сколько – на теплоходе, если известно, что на теплоходе он ехал на 3ч меньше, чем на поезде?
№5 При каких значениях а верно неравенство
- а2
Контрольная работа №10 по теме: «Раскрытие скобок. Подобные слагаемые».
Вариант 2
№1 Найдите значение выражения:
А) 17,8 – (11,7 + 14,8) – (3,5 – 12,6)
Б) 21,4 + (12,3 – 27,9) – (4,6 -0,3)
№2 Упростите выражение и найдите значение:
А) 0,9х + 1,3у -34 -0,6у + 0,6х – 0,7у + 20
при х= - 40 и у= -10,01
Б) 5k – (3k – 8p), если k+4p=17
№3 Решите уравнение:
А) 0,18х - 0,19х – 3,54 = - 2,89
Б) 0,6(х + 7) – 0,5(х – 3) = 6,8
№4 Решите задачу: первый участок пути мотоциклист ехал со скоростью 42 км/ч, а второй – со скоростью 30км/ч. Всего он проехал 159 км. За сколько времени мотоциклист проехал первый участок пути и за сколько второй, если на первый участок он затратил на 0,5 ч меньше, чем на второй?
№5 При каких значениях с верно неравенство
c2?
Контрольная работа № 11 : «Решение уравнений»
Вариант №1
1.Решить уравнение
А) 9х-7=6х+14 б)3(4х-2)+6=-2х+4
2. Проволоку длиной 456 м разрезали на 3 куска, причем первый кусок в 4 раза длиннее третьего, а второй на 114 м длиннее третьего.Найти длину каждого куска.
3.Решить уравнение
А) -
= 5 б) 0,2(7-2у)=2,3-0,3(у-6)
4.В первом ящике было в 7 раз больше гвоздей, чем во втором. Когда из первого ящика взяли 38 кг гвоздей, а из второго 14кг, то во втором осталось на 78 кг меньше, чем в первом. Сколько гвоздей было первоначально в каждом ящике?
5. Дано уравнение ах=-4.
Укажите значения а, при котором:
1)уравнение не имеет корней;
2) укажите все целые значения а, при которых корнем уравнения является натуральное число.
Вариант №2
1.Решить уравнение
А) 11х-9=4х+19 б)7х-15=5х+5(2х+1)
2. Трое рабочих изготовили всего 762 детали, причем второй изготовил в 3 раза больше деталей, чем третий, а первый на 117 деталей больше, чем третий. Сколько деталей изготовил каждый?
3.Решить уравнение
А) -
= 7 б) 0,3(8-3у)=3,2-0,8(у-7)
4.В первом шкафу было в 6 раз больше книг, чем во втором. Когда из первого шкафа взяли 46 книг, а из второго 18, то во втором осталось на 97 книг меньше, чем в первом. Сколько книг было первоначально в каждом шкафу?
5. Дано уравнение ах=-8.
Укажите значения а, при котором:
1)уравнение не имеет корней;
2) укажите все целые значения а, при которых корнем уравнения является натуральное число.
Итоговая контрольная работа.
Вариант 1
1.Сколько граммов содержится в 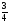 кг?
кг?
2.Какое из чисел наименьшее ?
3.Вычислите 3
; (
.
4.В коробке было 30 конфет, 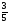 из них съели. Сколько конфет съели?
из них съели. Сколько конфет съели?
5.Какова скорость автомобиля, если он проехал 75 км за 1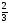 часа?
часа?
6.Начертите равнобедренный треугольник и найдите его периметр.
7.Две машинистки одновременно начали печатать рукопись и через 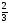 часа закончили работу. Сколько страниц в рукописи, если известно, что первая машинистка печатает 12 страниц в час, а вторая – 9 страниц в час.
часа закончили работу. Сколько страниц в рукописи, если известно, что первая машинистка печатает 12 страниц в час, а вторая – 9 страниц в час.
8.Какая из данных дробей расположена на координатной прямой между дробями
Итоговая контрольная работа.
Вариант 2
1.Сколько метров содержится в 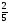 км?
км?
2.Какое из чисел наибольше ?
3.Вычислите 4
; 1 - (
4.В коробке было 40 конфет, из них съели. Сколько конфет съели?
5.Сколько стоит 1 кг апельсинов, если за 1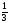 кг заплатили 60 рублей?
кг заплатили 60 рублей?
6.Начертите прямоугольный треугольник и найдите его периметр.
7.мастер делает 20 деталей в час, а ученик только 12. Работая одновременно, мастер и ученик выполнили заказ по изготовлению деталей за 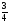 часа. Сколько деталей изготовили мастер с учеником?
часа. Сколько деталей изготовили мастер с учеником?
8.Какая из данных дробей расположена на координатной прямой между дробями
?



 и его применение при вычислениях.
и его применение при вычислениях.





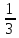 прямоугольника.
прямоугольника.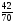 .
.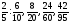 .
. 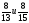
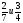 к общему знаменателю
к общему знаменателю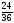
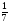 , но меньше
, но меньше 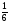 .
.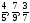 .
.
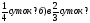
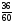 .
.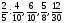 .
. 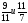
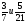 к общему знаменателю
к общему знаменателю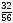
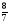
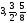 .
.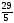 .
.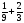 ; б)
; б) 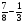 ; в) 2
; в) 2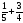 ; г)2-1
; г)2-1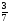
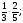 б)
б) 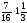 ; в) 10
; в) 10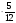 ; г)
; г) 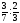 ; д)
; д) 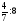 .
.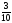 кг больше. Сколько килограммов яблок в двух пакетах
кг больше. Сколько килограммов яблок в двух пакетах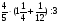
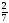 . Выделите целую часть
. Выделите целую часть 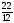 .
.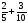 ; б)
; б) 



