
ГИА МАТЕМАТИКА

Содержание ( виды заданий В8)
- Найдите значение производной функции в точке х 0 по рисунку с изображенным графиком функции y = f(x) и касательной к нему в точке с абсциссой х 0 .
- На рисунке изображен график функции y = f (x) , касательная к этому графику, проведенная в точке х 0 , проходит через начало координат. Найдите f ' (х 0 ).
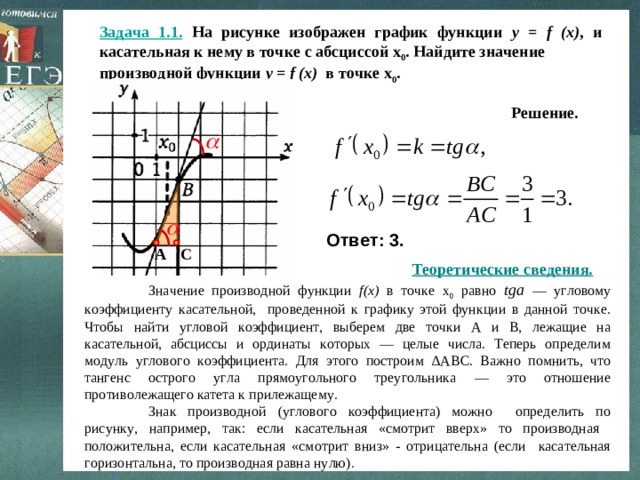
Задача 1.1. На рисунке изображен график функции y = f (x) , и касательная к нему в точке с абсциссой х 0 . Найдите значение
производной функции y = f (x) в точке х 0 .
Решение.
Ответ: 3.
С
А
Теоретические сведения.
Значение производной функции f(x) в точке х 0 равно tga — угловому коэффициенту касательной, проведенной к графику этой функции в данной точке. Чтобы найти угловой коэффициент, выберем две точки А и В, лежащие на касательной, абсциссы и ординаты которых — целые числа. Теперь определим модуль углового коэффициента. Для этого построим ∆ ABC. Важно помнить, что тангенс острого угла прямоугольного треугольника — это отношение противолежащего катета к прилежащему.
Знак производной (углового коэффициента) можно определить по рисунку, например, так: если касательная «смотрит вверх» то производная положительна, если касательная «смотрит вниз» - отрицательна (если касательная горизонтальна, то производная равна нулю).
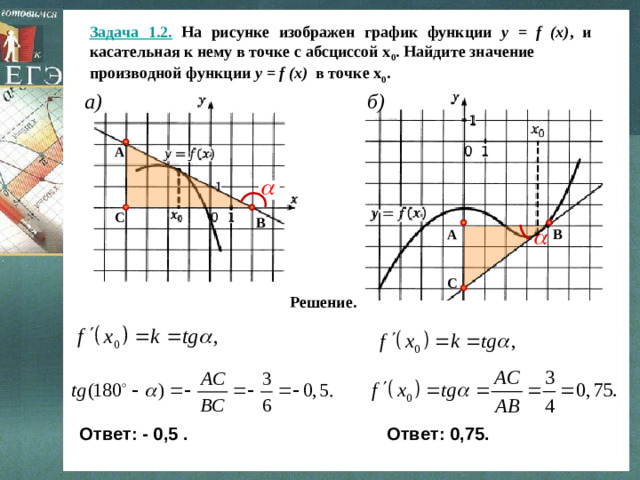
Задача 1.2. На рисунке изображен график функции y = f (x) , и касательная к нему в точке с абсциссой х 0 . Найдите значение
производной функции y = f (x) в точке х 0 .
a)
б )
А
С
В
А
В
С
Решение.
Ответ: - 0,5 .
Ответ: 0,75.
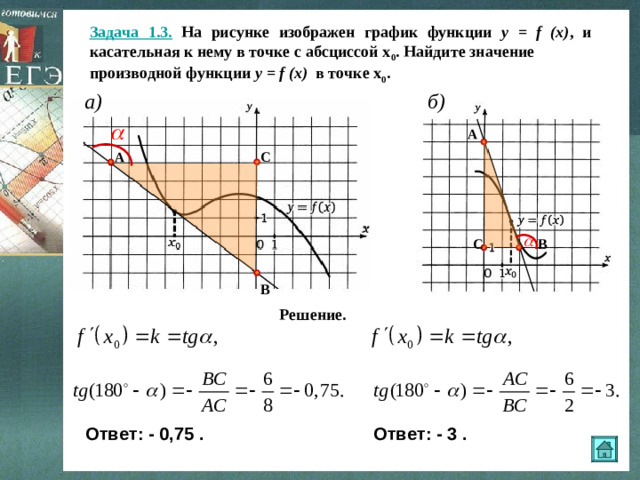
Задача 1.3. На рисунке изображен график функции y = f (x) , и касательная к нему в точке с абсциссой х 0 . Найдите значение
производной функции y = f (x) в точке х 0 .
б )
a)
А
А
С
В
С
В
Решение.
Ответ: - 0,75 .
Ответ: - 3 .
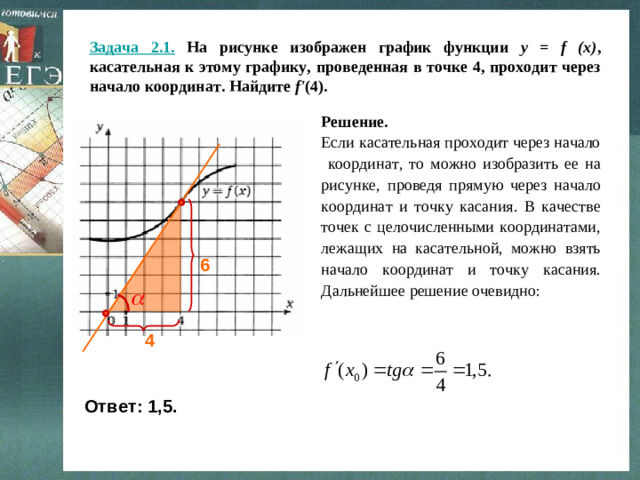
Задача 2.1. На рисунке изображен график функции y = f (x) , касательная к этому графику, проведенная в точке 4, проходит через начало координат. Найдите f ' (4).
Решение.
Если касательная проходит через начало координат, то можно изобразить ее на рисунке, проведя прямую через начало координат и точку касания. В качестве точек с целочисленными координатами, лежащих на касательной, можно взять начало координат и точку касания. Дальнейшее решение очевидно:
6
4
Ответ: 1,5.
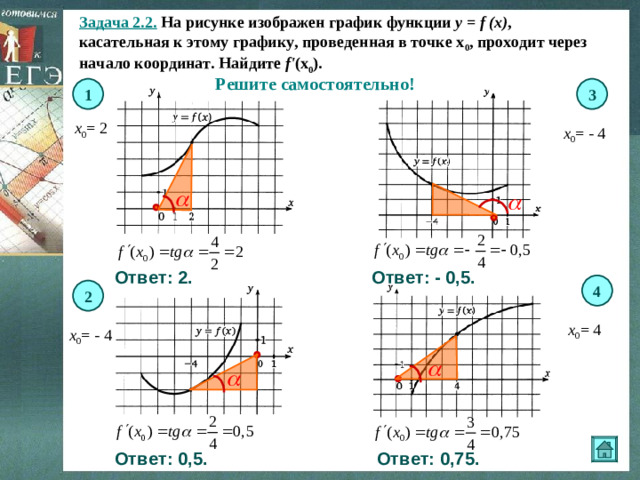
Задача 2.2. На рисунке изображен график функции y = f (x) , касательная к этому графику, проведенная в точке х 0 , проходит через начало координат. Найдите f ' (х 0 ).
Решите самостоятельно!
1
3
х 0 = 2
х 0 = - 4
Ответ: - 0,5.
Ответ: 2.
4
2
х 0 = 4
х 0 = - 4
Ответ: 0,5.
Ответ: 0,75.







