Практическая работа по теме: «Решение линейных уравнений, систем уравнений и неравенств»
Цель :
- Повторить знания обучающихся в теме: «Решение линейных уравнений, систем уравнений и неравенств».
Закрепить умения и навыки решения линейных уравнений, систем уравнений и неравенств .
Определить уровень усвоения знаний, оценить результат деятельности обучающихся.
Оборудование: рабочие тетради и тетради для практических работ, ручка, калькулятор.
Продолжительность: 1 час
Порядок выполнения:
Ознакомиться с теоретическим материалом и решением примеров .
Сделать краткий конспект теоретического материала в рабочих тетрадях (основные понятия, определения, формулы, примеры).
В тетрадях для практических работ выполнить практическую работу .
Теоретические сведения:
Линейные уравнения.
Уравнение вида ax+ b=0, где a и b — некоторые постоянные, называется линейным уравнением.
Если a0, то линейное уравнение имеет единственный корень: x =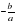 
.
Если a=0; b 0, то линейное уравнение решений не имеет.
Если a=0; b = 0, то, переписав исходное уравнение в виде ax = -b, легко видеть, что любое x является решением линейного уравнения.
Решить уравнение — значит найти все его корни или доказать, что корней нет.
При решении уравнений используются следующие свойства:
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получите уравнение, равносильные данному.
Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Примеры решения уравнений
| № п/п | Пример | Решение |
| 1 | 2x – 3 + 4(x – 1) = 5 | Пос Последовательно раскроем скобки, приведём подобные члены и найдём x: 2x – 3 + 4x – 4 = 5 2x + 4x = 5 + 4 + 3, x = 2. Ответ: 2. |
| 2 | -8(11-2х)+40=3(5х-4) | Раскроем скобки в обеих частях уравнения, перенесем все слагаемые с х в левую часть уравнения, а слагаемые, не содержащие х, в правую часть, получим: х=36 Ответ: 36. |
| 3 | 2x – 3 + 2(x – 1) = 4(x – 1) – 7 | 2x + 2x – 4x = 3 +2 – 4 – 7 0x = – 6 Ответ: |
| 4 | 2x + 3 – 6(x – 1) = 4(x – 1)+ 5 | 2x – 6x + 3 + 6 = 4 – 4x + 5 |
Системы уравнений с двумя переменными
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство. Решить систему — значит найти все ее решения или доказать, что их нет.
При решении линейных систем используют метод подстановки и метод сложения.
Примеры решения систем уравнений
|
| Пример | Решение |
|
5 |
| Для решения этой системы применим метод подстановки. Выразим из первого уравнения х и подставим это значение
|
| 6 |
| Для решения этой системы применим метод сложения уравнений. 8х=16, х=2. Подставим значение х=2 в первое уравнение, получим 10-у=9, у=1. |
| 7 |
| Эта система равносильна одному уравнению 2х+у=5, т.к. второе уравнение получается из первого умножением на 3. Следовательно, ей удовлетворяет любая пара чисел (х; 5-2х). Система имеет бесконечное множество решений. |
| 8 |
| Умножим первое уравнение на –2 и сложим С со вторым уравнением, получим 0×х+0×у=-6. Этому у уравнению не удовлетворяет ни одна пара чисел. Сл Следовательно, эта система не имеет решений. |
Линейные неравенства с одной переменной.
Линейным называется неравенство вида ax+b0 (соответственно ax+b 0, ax+b 
0), где а и b – действительные числа, причем а
0.
Неравенства решаются на основе следующих утверждений.
Теорема 1. Если какой-либо член неравенства с одной переменной перенести из одной части неравенства в другую с противоположным знаком, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному.
Теорема 2. Если обе части неравенства с одной переменной умножить или разделить на одно и то же положительное число, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному.
Теорема 3. Если обе части неравенства с одной переменной умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное данному.
Примеры решения неравенств
|
| Пример | Решение |
| 9 | 2(х-3)+5(1-х) | Раскрыв скобки, получим 2х-6+5-5х -9х |
| 10 |
| Освободимся от знаменателей, для чего умножим обе части неравенства на положительное число 6, оставив без изменения знак неравенства:
Далее последовательно получаем:
Последнее неравенство верно при любом значении х, так как при любом значении переменной получается истинное высказывание 0-55. Поэтому множеством его решений служит вся числовая прямая. |
Система неравенств
Говорят, что несколько неравенств с одной переменной образуют систему, если ставится задача найти множество общих решений заданных неравенств.
Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называется решением системы неравенств.
Множество решений системы неравенств есть пересечение множеств решений неравенств, образующих систему. Неравенства, образующие систему, объединяются фигурной скобкой.
Пример решения систем неравенств
|
| Пример | Решение |
| 11 |
|
С помощью числовой прямой находим, что пересечением этих множеств служит интервал |
Варианты практической работы:
| Вариант 1 | Вариант 2 |
| 1.Решите уравнение | |
| а) |
|
| б) | |
| в) | |
| г) | |
| д) |
|
| 2.Решите неравенство | |
| а) |
|
| б) |
|
| 3.Решите систему уравнений | |
| а) б) |
|
| 4.Решите систему неравенств | |
|
|
|
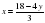
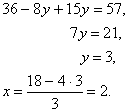
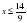
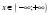
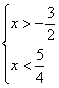
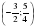
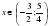
методом сложения
методом подстановки
методом сложения
методом подстановки
