Конспект урока в 7 А классе по теме:
«Сумма углов треугольника» (на доске)
Тип урока: открытия нового знания
Цели урока: организовать деятельность учащихся по восприятию теоремы о сумме углов треугольника, ее доказательству, осмыслению и применению в решении задач.
Планируемые результаты:
Предметные:
Знать формулировку и доказательство теоремы о сумме углов треугольника.
Уметь решать задачи на нахождение углов треугольника.
Личностные:
Уметь проводить самооценку на основе критерия успешности учебной деятельности.
Метапредметные:
Уметь определять и формулировать цель на уроке с помощью учителя; работать по коллективно составленному плану; оценивать правильность выполнения действий на уровне адекватной ретроспективной оценки; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение (Регулятивные УУД).
Уметь оформлять свои мысли в устной и письменной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им (Коммуникативные УУД).
Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке (Познавательные УУД).
Мотивация к учебной деятельности. (2 мин)
- Здравствуйте, ребята!
- Что мы делали на прошлом уроке? (Обобщали и закрепляли знания по теме «Параллельность двух прямых».)
- Какие прямые называются параллельными?
- Правильно. Что вам помогает утверждать, что прямые параллельны? (Признаки параллельности прямых...)
Настраиваемся на рабочую волну и стремимся по ступеням знаний к новым открытиям. (Слайд 2)
Девиз сегодняшнего урока:
НАБЛЮДАЮ – ЗАМЕЧАЮ – РАЗМЫШЛЯЮ – ДЕЛАЮ ВЫВОД (на доске)
Принципы урока:
Равенство всех участников
Все способны, все могут всё
Полная свобода мнений
Доброжелательность
Знания одного должны быть обогащены знаниями других
Но прежде чем мы приступим к работе, подпишите листы самооценки, лежащие у вас на столах.
- Итак, начнём.
Актуализация знаний и фиксирование индивидуального затруднения (5 мин)
| Деятельность учителя | Деятельность ученика | ИКТ |
| Давайте вспомним, как называются углы, образованные при пересечении двух прямых третьей? Назовите пары углов, указанные на слайде. | Отвечают: односторонние, накрест лежащие, соответственные.
Называют пары углов
|
|
| Сформулируйте признаки параллельности двух прямых. Параллельны ли прямые указанные на слайдах?
| Формулируют признаки.
Отвечают, обосновывают ответы. |
|
| Сформулируйте теоремы об углах, образованных двумя параллельными прямыми и секущей. Найдите углы, указанные на слайдах. | Формулируют теоремы.
Находят углы. |
|
| Сколько прямых, параллельных стороне АС, можно провести через вершину В? | Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.(аксиома параллельных прямых).
Отвечают (одну) |
|
| Как можно найти углы треугольника, если будут известны углы 1, 2 и 3?
| Отвечают (через знания углов, образованные двумя параллельными прямыми и секущей)
Пусть угол 1 равен 50̊, угол 2 равен 60̊, а угол 3 равен 70̊. Найдите углы треугольника. И тогда сумма углов данного треугольника равна ? (180̊) |
|
|
| ||
| Как еще можно измерить углы треугольника? Случайно ли сумма углов этого треугольника оказалась равной 180 ̊ или этим свойством обладает каждый треугольник? Это утверждение носит название теоремы о сумме углов треугольника. Итак, как вы думаете, какова тема нашего урока? Откройте тетради и запишите её. Цели и задачи нашего урока?
|
Отвечают: с помощью транспортира
У каждого треугольника сумма углов равна 180 ̊.
Сумма углов треугольника. |
|
Усвоение новых знаний. (8 мин)
Приступаем к выполнению этих задач. Начнем с практических заданий.
Выполните задание, указанное на слайде. Результаты занесите в таблицу.
Выполняют задание

Выполните задание, указанное на слайде. Отрежьте углы своего треугольника, не забывая о технике безопасности при работе с ножницами. Сделайте вывод.
Давайте сравним полученные результаты. Какие мысли у вас возникают?
- нет огромной разницы между полученными данными;
- все треугольники были разными, а результаты почти одинаковые;
- можно предположить, что сумма углов треугольника равна 180˚;
- неужели у всех треугольников сумма углов является одной и той же величиной?
Итак, мы выдвинули гипотезу, что сумма углов треугольника равна 180˚. Но это только наше предположение. (Сумма углов треугольника была практическим путём установлена, вероятно, ещё в Древнем Египте. Прокол утверждал, что доказательство этого факта было известно ещё в V в. до н.э.)
Если сумеем это утверждение доказать с помощью математических рассуждений, то это будет математический факт.
Вернитесь к 1 и 2 исследовательским заданиям. Если у вас получилась, что сумма углов треугольника равна 1800, то в листе самооценки поставьте за каждое исследование по 1 баллу. В противном случае поставьте 0 баллов.
-Кто себе поставил по одному баллу? Встаньте!
С чего мы начинаем доказательство теоремы? ( Записываем, что дано и чертим чертёж)
- Что нам дано? ( Произвольный треугольник)
-Что надо док-ть? (сумма углов =1800)
 Учитель чертит на доске произвольный треугольник.
Учитель чертит на доске произвольный треугольник.Обозначим его АВС.
Для удобства обозначим углы треугольника 1,2 и 3.
Достаточно ли нам данного чертежа, чтобы доказать теорему?
Что вы можете предложить?
Достаточно ли введённых обозначений?
- Что теперь необходимо сделать? (Составить план действий по реализации сформулированной цели.)
- Прежде, чем приступить к составлению плана, ответьте на вопрос «Какие вы знаете углы, которые в сумме составляют 180о?» (Сумма смежных углов, развернутый угол и сумма внутренних односторонних углов, образованных при пересечении параллельных прямых секущей, равна 180о.)
- У вас в группах лежат шаги будущего плана доказательства теоремы. Прочтите эти шаги и расставьте их в нужном порядке.
Составьте план доказательства этой теоремы, запишите его в тетради, выполните дополнительные построения (при необходимости можно обратиться к учебнику - страница 69)
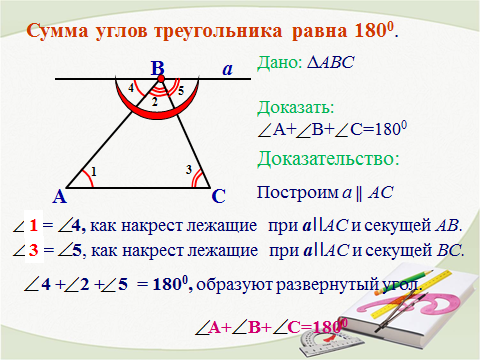
Докажите теорему о сумме углов треугольника.
Выполняют задание, делают вывод.
Отвечают: Сумма углов треугольника равна 1800.
Отвечают: у каждого треугольника сумма углов равна 1800.
Это утверждение носит название теоремы о сумме углов треугольника.
Заполняют лист самооценки.
После обсуждения на доске фиксируется план действий:
1. Провести через вершину треугольника прямую, параллельную противоположной стороне.
2. Рассмотреть накрест лежащие углы при параллельных прямых и секущей.
3. Провести аналогию между углами, на которые разбит развернутый угол и углами треугольника. (заготовка)
Работа организуется в группах, одна из групп озвучивает результат работы, остальные при необходимости уточняют, дополняют.
Один ученик доказывает теорему.

Релаксация (физминутка).(1 мин)
Первичное закрепление.(8 мин)
| Мы доказали одну из основных теорем геометрии. Что она утверждает? Ответьте на вопросы устно:
5. В каком треугольнике сумма углов больше: в остроугольном или тупоугольном треугольнике? 6. Можно ли измерить углы любого треугольника? (Это один из самых загадочных и интересных треугольников. Еще это место называют аномальной зоной) Найдите неизвестные углы в треугольниках.
|
Отвечают.
Нет. Например, существует Бермудский треугольник, который находится в Атлантическом океане между Бермудскими островами, государством Пуэрто-Рико и полуостровом Флорида, у которого невозможно измерить углы.
|
|
| Самостоятельно найдите неизвестные углы в треугольниках.
Поменяйтесь тетрадями с соседом по парте. Сверьте решения, если вы с чем – то не согласны обсудите это с соседом, выясните кто из вас прав. Проверьте решения соседа, каждое правильное решение оцените 1 баллом и зафиксируйте результат в его листе самооценки
|
Решают задачи
Работают в парах
Проверяют, оценивают решения и фиксируют результат в листе самооценки
|
|
|
7. Организация первичного контроля (проверка через презентацию) (5 мин)
| ||
| Проверьте себя, ответьте на вопросы теста.
Проверьте свои ответы, каждый правильный ответ оцените 1 баллом и результат зафиксируйте в листе самооценки.
| Выполняют тест
Проверяют ответы и фиксируют результат в листе самооценки
|
|
Итог урока. (5 мин)
Итак, ребята мы заканчиваем наш урок. Вы сегодня хорошо потрудились. Сами доказали теорему о сумме углов треугольника. Так чему же равна сумма углов любого треугольника? Давайте вернемся к вашим оценочным листам и подведем результаты.
Оцените свою работу, согласно критериям, указанным на слайде (Оценивают работу, фиксируют в листе самооценки). Кто получил «5», встаньте, «4», «3»?
Рефлексия.
А теперь я прошу вас выбрать по 1-2 предложения и закончить их. (Каждый ученик выбирает по 1-2 предложения и заканчивает их.)
Домашнее задание.
На «3»: п.30, 31. № 223 ( а, б).
На «4»: п.30, 31. № 223 ( а, б); № 224.
На «5»: п.30, 31. № 223 ( а, б); № 224;
приготовить кластер: разновидности треугольника в зависимости от его сторон и углов.
Закончить урок мне хочется словами одного мудреца:
«Высшее проявление духа - это разум. Высшее проявление разума - это геометрия. Клетка геометрии - треугольник. Он так же неисчерпаем, как и Вселенная».
Надеюсь, наш урок подтверждает эти слова.
Спасибо всем за урок.














 Учитель чертит на доске произвольный треугольник.
Учитель чертит на доске произвольный треугольник.












