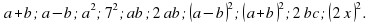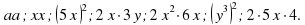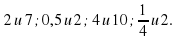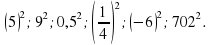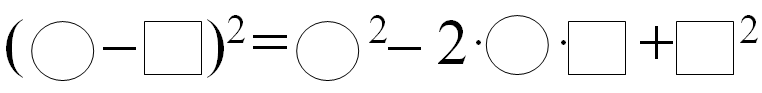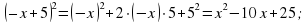Квадрат суммы и квадрат разности

Урок алгебры в 7 классе

Тема: Квадрат суммы и квадрат разности

Цели:

Образовательные: добиться осознанного понимания учащимися содержания формул «квадрат суммы» и «квадрат разности двух выражений»; сформировать первичные умения применения этих формул для преобразования квадрата двучлена в многочлен стандартного вида.

Развивающие: вырабатывать умения анализировать и сравнивать, развивать вычислительные навыки.

Воспитательные: воспитывать сознательное отношение к учебному труду, формировать жизнеспособные компетенции личностной деятельности: умение анализировать её, оценивать и планировать.

Метапредметные: формировать умения обрабатывать информацию; формировать коммуникативную компетенцию учащихся и умение выбирать способы решения задач в зависимости от конкретных условий.

Тип урока: усвоение новых знаний

Ход урока.

1. Организационный момент, постановка учебной задачи.

На столах у вас лежат листы самооценивания. Подпишите их. В течение урока мы с вами будем выполнять различные задания. По окончанию решения каждой задачи, вы должны оценить свою работу:

«+» – справился с задачей без затруднений,

«±» – справился с задачей, но возникали сложности,

«–» – не справился с задачей.

1. Актуализация опорных знаний (устная работа)

1. Прочитайте выражение, используя понятия «сумма», «разность» «произведение», «квадрат» и т.д.:

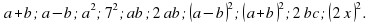
2. Упростите выражения:

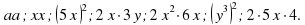
3. Вычислите для каждой пары чисел произведение и удвоенное произведение:

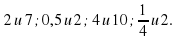
4. Вычислите

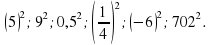
Последнее выражение не смогли вычислить устно? Почему? В конце урока мы вернемся к этому заданию.

1. Сообщение темы, цели урока, мотивация учебной деятельности. Тема сегодняшнего урока: «Квадрат суммы и квадрат разности двух выражений»

Какие же задачи на урок вы себе ставите? {ученики пробуют формулировать задачи}

1. Усвоение новых знаний.

   1. Объяснение учителя с элементами беседы.

Квадрат суммы двух выражений имеет вид Применим ранее изученный материал:

.

Обратите внимание на правые части, сколько слагаемых в каждом из них

Как можно назвать первое слагаемое? Второе слагаемое? Третье слагаемое?

Получилась формула. Как можем назвать эту формулу?

Данное тождество называется формулой квадрата суммы.

1. Работа с учебником, 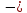знакомимся с словесной формулировкой данного тождества. (стр.164).

2. Аналогично, можно вывести формулу квадрата разности двух выражений. Работу выполняет ученик на доске.

.

1. Для работы с данной формулой можно использовать общую модель. (модель заранее начертить на картоне или оформить на магнитной доске)

2. Выполнение тренировочных упражнений №№ 800(а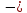г), 803 (ав), 810(е).

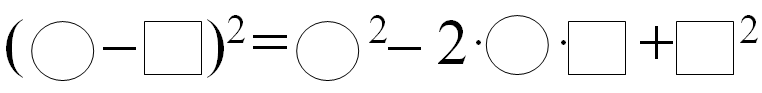
При выполнении заданий ученики проговаривают словесную формулировку и заполняют схему на доске и на черновиках.

Записи в тетрадях:

№ 800.

№803

№810

1. Физкультминутка

Поднимает руки класс – это «раз».
Повернулась голова – это «два».
Руки вниз, вперед смотри – это «три».
Руки в стороны по - шире развернули на «четыре»,
С силой их к плечам прижать – это «пять»
Всем ребятам надо сесть – это «шесть».

1. Выполнение письменных упражнений в парах №805(а, б), №805 (в, г)

   1. 

   2. ;

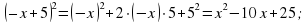
Выполнив задания, ученики сравнивают условия и полученный результат.

1. Докажем тождества

; .

Задание: Каждому члену группы оценить результат своей работы, обозначая правильно решённый пример знаком + или – . Определить уровень своих учебных достижений. Самооценка самостоятельной работы (отметка в столбике «самостоятельная работа» листа оценки).

1. Рефлексия. Прием «Незаконченное предложение» (по памятке). Заполнение листов самооценки.

Выбор «кружка»: зеленый, если все было понятно, «думаю, что затруднений с домашним заданием не возникнет»; желтый – есть затруднения, красный – было трудно.

1. Домашнее задание. Выучить две формулы и их словесные формулировки

Зеленый цвет – №№ 804,810 (д);

желтый – № 800 (дз); 810(в);

красный – №799(а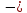д). (по учебнику Алгебра, 7 класс, авт. Ю.Н. Макарычев и др. )

Словесная самооценка (Памятки в помощь)

Сегодня я узнал…

Было интересно…

Было трудно…

Я выполнял задания…

Я понял, что… теперь я могу…

Я приобрел…