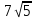Полугодовая контрольная работа по Алгебре
для учащихся 8 классов
Вариант I
№1. Сократите дробь: а)  ; б)
; б) 
№2. Упростите выражение: а)  :
:
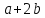 ; 2) 2; 3)
; 2) 2; 3) 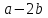 ; 4)
; 4) 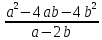
Б)  .
.
1)  2)
2)  ; 3)
; 3)  4)
4) 
№3.Вычислите: а)  ; б)
; б) при
при 
№4. Вынесите множитель за знак корня 
21; 2) 13; 3)
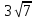 ; 4)
; 4) 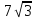
№5. Решите уравнение  . Если уравнение имеет несколько корней, то в ответе запишите наибольший.
. Если уравнение имеет несколько корней, то в ответе запишите наибольший.
№6. Установите соответствие между графиками функций и формулами, которые их задают.
| А | Б | В |
|
|
|
|

 ; 2)
; 2)  ; 3)
; 3) 
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
№7. На рисунке жирными точками показана цена нефти на момент закрытия биржевых торгов во все рабочие дни с 17 по 31 августа 2004 года. По горизонтали указываются числа месяца, по вертикали — цена барреля нефти в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наименьшую цену нефти на момент закрытия торгов в указанный период (в долларах США за баррель).
№8. Недельное домашнее задание по математике Лина выполнила за 3 дня, а Маша это же задание выполнила за 5 дней. Сколько задач в один день решала Маша, если она решала на 4 задачи меньше, чем Лина? Обозначив за х число задач, которые решала за один день Маша, можно составить уравнение:
1) 5(х + 4) = 3х 2) 5х – 3х = 4
3) 5х + 3х = 4 4) 5х = 3(х + 4)
№9. Тетрадь стоит 40 рублей. Какое наибольшее число таких тетрадей можно будет купить на 750 рублей после понижения цены на 10%?
№10. 
Полугодовая контрольная работа по Алгебре
для учащихся 8 классов
Вариант II
№1. Сократите дробь: а)  ; б)
; б) 
№2. Упростите выражение: а)  :
:
1) ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 
Б) 

1) −20b² + 14b + 49  2) −20b² + 14b − 49
2) −20b² + 14b − 49 ; 3) −20b² + 49.
; 3) −20b² + 49. 4)−20b² − 14b + 47.
4)−20b² − 14b + 47.
№3.Вычислите: а)  ; б)
; б)  при
при 
№4. Вынесите множитель за знак корня 
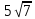 ; 2) 21; 3)
; 2) 21; 3) 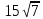 ; 4)
; 4) 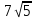
№5. Решите уравнение  . Если уравнение имеет несколько корней, то в ответе запишите наименьший.
. Если уравнение имеет несколько корней, то в ответе запишите наименьший.
№6. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
Графики
| А | Б | В |
|
|
|
|

Коэффициенты
| 1) k 0, b | 2) k | 3) k 0 | 4) k 0, b 0 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: 
№7. На рисунке жирными точками показана цена золота на момент закрытия биржевых торгов во все рабочие дни с 5 по 28 марта 1996 года. По горизонтали указываются числа месяца, по вертикали — цена унции золота в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена золота на момент закрытия торгов была наименьшей за данный период.
№8. Саша прочитал книгу за 5 дней, а Илья эту же книгу прочитал за 7 дней. Сколько страниц в один день читал Илья, если Саша читал в один день на 12 стр. больше, чем Илья. Обозначив за х число страниц, которые читал в один день Илья, можно составить уравнение:
1) 7 (х+12) = 5х 2) 7х – 5х = 12
3) 5х + 7х = 12 4) 7х = 5 (х + 12)
№9. Держатели дисконтной карты книжного магазина получают при покупке скидку 3%. Книга стоит 300 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
№10. Упростите выражение



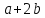 ; 2) 2; 3)
; 2) 2; 3) 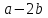 ; 4)
; 4) 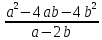
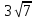 ; 4)
; 4) 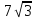
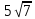 ; 2) 21; 3)
; 2) 21; 3) 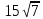 ; 4)
; 4)