Разработка урока по алгебре 7 класса :
«Действия над многочленами»
урок повторения
Составил: учитель математики и физики Тхитлянова Ю.Ш.
ХОД УРОКА
1.Организационный момент
Здравствуйте ребята. Сегодня у нас урок закрепления материала по теме «Действия с многочленами». Девиз нашего урока «Дорогу осилит идущий, а математику мыслящий». Сегодня нам как раз нужно как можно более эффективно применять свойства нашего ума при решении примеров и заданий.
На нашем уроке мы проводим математический марафон. Марафон пройдет в несколько этапов.
Ребята, а давайте определим с вами задачи, которые должны решить на нашем уроке!
В ходе марафона мы должны: закрепить изученный материал, показать уровень усвоения темы, разобраться в непонятных ранее моментах, проконтролировать и оценить свои знания.
У каждого из вас на столе оценочный лист, где вы будете фиксировать свои достижения, и в конце оцените свою работу как марафонцы.
Оценочный лист
| 1 этап «Теоретический» | 2 этап «Практический» | 3 этап «Исследовательский» | 4 этап «Раскрытие тайн» | 5 этап «Решение уравнений» | Всего баллов |
Оценка |
|
|
|
|
|
|
|
|
НУ, что, приступим?!
II. Повторение основных понятий темы.
А сейчас открыли тетради и записали тему урока. Приступаем
I. этап – теоретический.
Математический диктант. Я читаю предложения. Если оно верно – ставьте плюс, если неверно – минус. Начнем:
1. Одночленом называют сумму числовых и буквенных множителей.
2. Одночлены, которые отличаются друг от друга только коэффициентами, называются подобными членами.
3. При умножении одночлена на одночлен получается одночлен.
4. Когда раскрываем скобки, перед которыми стоит знак « – », скобки надо опустить, сохранив знак каждого члена, который был заключен в скобки.
5. В результате умножения многочлена на одночлен получается одночлен.
6. Алгебраическая сумма нескольких одночленов называется многочленом.
7. Буквенный множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
8. Чтобы умножить одночлен на многочлен, надо этот одночлен умножить на каждый член многочлена и результаты сложить.
9. Многочлен, в котором отсутствуют подобные члены и каждый из них одночлен стандартного вида называется многочленом стандартного вида.
10. Чтобы раскрыть скобки, перед которыми стоит знак « + », скобки надо опустить, сохранив знак каждого члена, который был заключен в скобки.
Взаимопроверка: – + + – – + – + + +
3 балла – ошибок нет или 1 ошибка
2 балла – 2 – 3 ошибки
1 балл – 4 – 5 ошибок
II. этап - Математическое лото.
Учащимся предлагается большая карта с заданиями и маленькие карточки с разрезанными ответами. Выполнив задание на большой карте, необходимо найти результат на маленькой карточке и этой карточкой накрыть соответствующее задание на большой карте.
если рисунок получился, то учащийся получает оценку «5»,
1, 2 ошибки – оценка «4»,
меньше правильных ответов – оценка «3».
Вариант I
| Выполнить действие: (3х+10у) – (6х+3у) | Выполнить умножение: 6х2(5 – 3х) | Найдите недостающий множитель: а3(2а + …) = 2а4 + 5а6 |
| Привести к стандартному виду многочлен: – х + 5х2 + 3х3 + 4х – х2 | Выполнить умножение: (4х – 3)(8х + 6) | Выполнить действие: 3х2(2х – 0,5у) |
| Упростить выражение: 12х(х – у) – 6у(у – х) | Решить уравнение: 8х + 5(2 – х) = 13 | Преобразовать выражение в многочлен стандартного вида: (3х2 – 2)(х2 + 6) |
Карточки с ответами
| 7у – 3х | 30х2 – 18х3 | 5а3 |
| 3х3 + 4х2 + 3х | 32х2 – 18 | 6х3 – 1,5х2у |
| 12 х2 – 6ху – 6у2 | 1 | 3х4 + 16х2 – 12 |
Вариант II
| Выполнить действие: (2а – 1) + (3 + 6а) | Выполнить умножение: 7(а – b) | Найдите недостающий множитель: 2ас(ас + …) = 2а2с2 + 8ас4 |
| Привести к стандартному виду многочлен: 4х2 + 3х – 5х2 + х3 | Выполнить действие: 4а2(а – b) | Выполнить умножение: (х – 2)(х + 3) |
| Упростить выражение: 6а(a – b) – 3b(b – a) | Решить уравнение: 4(а –5) + a = 5 | Преобразовать выражение в многочлен стандартного вида: (4b2 – 1)(2b2 + 3) |
Карточки с ответами
| 8а + 2 | 7а – 7b | 4с3 |
| х3 – х2 + 3х | 4а3 – 4а2b | х2 + х – 6 |
| 6а2 – 3ab – 3b2 | 5 | 4b4 + 10b2 – 3 |
III. этап – исследовательский.
Владение математикой – это умение решать задачи, причём не только стандартные, но и требующие оригинальности, изобретательности, смекалки, находчивости.
У каждого из вас карточки с 6-ю равенствам, среди которых есть верные, а есть и неверные. Вам необходимо найти ошибки. Напротив, каждого равенства нужно написать верно или неверно. Назвать ошибки.
| Верно – неверно | |
| 1) 7а2(х–у)= 7х2а –7ау2 | неверно |
| 2) (3а2)2=27а4 | неверно |
| 3) (9 у2–3у+15)∙3у= 27 у3–9 у2+ 45 | верно |
| 4) 5а2+3а–7–5а3+3а2–3а–11= –5а3+8а4–18 | неверно |
| 5) –3с(с3+с–4)= –3с4–3с2+12с | верно |
| 6) (3b2+2b)+(2b2–3b–4) – (–b2+19) = 3b2+2b+2b2–3b–4+b2+19=6b2– b+15 | неверно |
В оценочный лист выставляем: 3 балла – 5 – 6 правильных ответов, 2 балла - за 4 правильных ответа, 1 балл – за 3 правильных ответа.
Мы преодолели третий этап. Впереди нас ждут еще более интересные задания.
IV. этап – этап раскрытия тайн.
Межпланетная станция, запущенная для изучения планеты Марс, произвела фотосъёмку её поверхности. Побывала на ней, взяла пробу грунта и вернулась на Землю. Вместе с пробами учёные обнаружили кусок твёрдого сплава с таинственными обозначениями. Так вот, учёные обратились к нам за помощью, чтобы мы объяснили, что обозначают эти таинственные знаки.
Найди неизвестный математический объект.
Задание выполняем по вариантам.
| 1 вариант | 2 вариант |
| 1) (b+c–m)∙*=ab+ac–am | 1) *∙(p–x+y)=ap–ax+ay |
| 2) *∙(ab–b2)=a3b–a2b2 | 2) *∙(x2–xy)=x2y2–xy3 |
| 3) (a–b)∙*=a3b–a2b2 | 3) (x–1)∙*=x2y2–xy2 |
| 4) М+(6х2–3ху)=х2–ху+у2 | 4) М–(4ху+3у2)=х2+ху–у2 |
| Ответы: 1) а, 2) a2, 3) a2b, 4) –5x2+2xy+y2 | Ответы: 1) a, 2) y2, 3) xy2, 4) x2+5xy+2y2 |
В оценочный лист поставить: если все верные – 3 балла, 3 верных – 2 балла, 2 верных – 1 балл.
V этап – Пит-стоп.
На профессиональном языке спортсменов, а сегодня у нас спортивно-математический урок, означает Остановка, смена комплектующих)))
Физминутка…..
VI. этап – этап решения уравнений
Выдающийся физик Альберт Эйнштейн – основоположник теории относительности - говорил так: «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно».
Давайте примем участие в работе этого этапа.
Выдающийся физик Альберт Эйнштейн – основоположник теории относительности - говорил так: «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно». Вот и займёмся уравнениями. На доске записаны 8 уравнений. Каждый из вас будет решать 2 уравнения. Затем нужно будет подойти к доске, отыскать полученный результат и прикрепить его обратной стороной (буквой) к своему уравнению. Если вашего результата нет, значит, уравнение решено неверно.
Реши уравнения
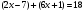 - А
- А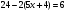 - Л
- Л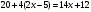 - Д
- Д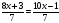 - Ж
- Ж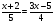 - А
- А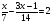 - Б
- Б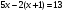 - Р
- Р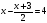 - А
- А
Сообщение учащегося:
Занимаясь математикой, мы не могли не заметить, что она состоит из нескольких частей. Мы научились оперировать с натуральными и дробными числами, знаем положительные и отрицательные числа. «Число» - по-гречески звучит арифмос. Поэтому наука о числе получила греческое название арифметика. Другой раздел математики посвящён различным фигурам и их свойствам и называется «Геометрия». Гео – по-гречески земля, метрио – мерею. Но вот слово алгебра – раздел математики, где решаются уравнения, рассматриваются преобразования выражений, составленные из чисел и букв – не греческое. В чём тут дело? Разве у греков не было алгебры. Была. Но решали древние греки алгебраические задачи геометрически.
А вот слово алгебра произошло от слова ал-джабра, взятого из названия книги узбекского математика, астронома и географа Мухамеда Ал-Хорезми «Краткая книга об исчислениях ал-джабры и ва-л-мукабалы». Арабское слово аль-джебр переводчик не стал переводить, а записал его латинскими буквами algebr. Так возникло название науки, которую мы изучаем. «Ал-джабра» – операция переноса отрицательных членов из одной части уравнения в другую, но уже с положительным знаком. По-русски это слово означает «восполнение».
Интересно, что «алгебраистами» в средние века называли вовсе не математиков, а арабских хирургов-костоправов. Об одном таком алгебраисте написал Сервантес в своём знаменитом романе «хитроумный идальго Дон Кихот Ламанчский»
Итак, кто решил 2 уравнения правильно, ставит в оценочные листы 3 балла, кто правильно решил 1 уравнение – ставит 2 балла.
Подведение итогов.
Конец урока.



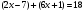 - А
- А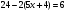
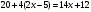
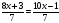 - Ж
- Ж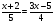 - А
- А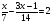 - Б
- Б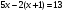 - Р
- Р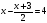 - А
- А



