Урок алгебри, 8 клас. № 36
Тема. Рівняння х2 = а. Основна тотожність квадратного кореня.
Мета.
Дидактична:повторити та узагальнити знання учнів щодо способу розв'язання рівняння виду х2 = а; сформулювати основну тотожність для квадратного кореня; формувати вміння розв'язувати рівняння виду х2 = а, а також рівняння, що зводяться до таких шляхом рівносильних перетворень;
Розвивальна: розвивати в учнів уміння застосовувати апарат математичної логіки для аналізу складних суджень, складання умовиводів.
Виховна: виховувати в учнів наукове розуміння процесу пізнання.
Повторення. Додавання і віднімання дробів з різними знаменниками.
Тин уроку: повторення та узагальнення знань, застосування знань та вмінь.
Хід уроку
I. Організаційний стан
II. Перевірка домашнього завдання
Перевірити наявність у зошитах домашнього завдання. Вияснити, чи були труднощі при виконанні.
Повторення. Фронтальна бесіда.
Пригадаємо алгоритм виконання додавання раціональних дробів з різними знаменниками.
III. Формулювання мети і завдань уроку.
Розглянути питання, чи можна графічно розв’язати рівняння х2 = а.
Скільки може бути розв’язків?
Відшукання відповіді на питання:
як знайти корені рівняння х2 = а, використовуючи дію добування квадратного кореня з числа;
як ще можна використати означення арифметичного квадратного кореня з числа;
становить мету уроку.
IV. Актуалізація опорних знань та вмінь.
Виконання усних вправ
Визначте сторони квадрата, площа якого дорівнює:
36 см2; 0,81 дм2; 1 м2; 900 мм2?
Обчисліть АКК із чисел: 4; 9; 0,25; 0,81; 0,64;
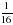 ;
; 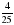 ;
; 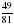 ; 3
; 3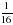 .
.Скільки спільних точок має графік функції у = х2 із прямою:
а) у = 4; б) у = 0,9; в) у = 0; г) у = -2; д) y = 3?
V. План вивчення нового матеріалу
Доведення того, то при а 0 корені рівняння х2 = а х1 і х2 дорівнюють відповідно
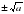 .
.Загальна схема розв'язання рівняння х2 = а.
Формулювання та доведення основної тотожності для квадратного кореня.
VI. Формування вмінь
Виконання усних вправ
Скільки коренів мають рівняння:
х2 = 9; х2 = -9; х2 = 3; х2 = 0; х2 – 31 = 0; х2 = – 31?
Знайдіть корені рівнянь:
х2 = 16; у2 = 0,81; z2 = -4; m2 = 5; n2 =  ; d2 = π.
; d2 = π.
Виконання письмових вправ
1) Розв'яжіть рівняння: а) х2 = 121; б) х2 = 0,16; в) х2 = 5; г) х2 = 0,3;
д) х2 =  ; є) х2 =
; є) х2 =  ; ж) х2 = -1; з) х2 = 1,44.
; ж) х2 = -1; з) х2 = 1,44.
2) Розв'яжіть рівняння:
а) 3х2 = 48; б) х2 + 8 = 57; в) 44 – х2 = 8; г) -2х2 = 18; д) -0,4х2 = -8;
є)  х2 = 1; ж) 12 + 3х2 = 6; з) 2(х2 + 1) = 10.
х2 = 1; ж) 12 + 3х2 = 6; з) 2(х2 + 1) = 10.
2) Розв'яжіть рівняння:
а) (х – 3)2 = 25; б) (х + 4)2 = 9; в) (х – 6)2 = 7; г) (х + 2)2 = 6.
2) Розв'яжіть рівняння: а)  ; б)
; б)  ;
;
в)  +
+ = 0; г)
= 0; г)  +
+ = 0.
= 0.
VII. Підсумки уроку
В якому з випадків правильно розв'язано рівняння?
| а) х2 – 5 = 0, -5 | б) х2 – 5 = 0, х2 = 5, | в) х2 – 5 = 0, х2 = 5, |
| коренів немає. | х = | х = |
| Відповідь. Коренів немає | Відповідь. | Відповідь. |
VІII. Рефлексія. Вправа «Пакуємо валізи».
Учням пропонується продовжити речення
Я дізнався…
Мені стало відомо…
Мене зацікавило…
Мене здивувало…
IX. Домашнє завдання.
Вивчити теоретичний матеріал уроку (див. конспект).
Повторити: властивості степеня з натуральним показником (див. 7 клас).
Розв’язати вправи: № 404, № 406.



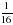 ;
; 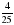 ;
; 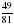 ; 3
; 3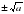 .
. .
. .
.



